
分析 去掉绝对值,写成分段函数的形式,结合图象分类求值域.
解答 解:f(x)=f(x)=x2+a|x-1|+1=$\left\{\begin{array}{l}{{x}^{2}+ax-a+1…x≥1}\\{{x}^{2}-ax+a+1…x<1}\end{array}\right.$
①当a=0时,f(x)=x2+1,f(x)min=1…(3分)
②当a>0时,结合图象
( i)当$\frac{a}{2}≥1$,即a≥2时,f(x)min=分(1)=2;…(6分)
( ii)当$\frac{a}{2}<1$,即0<a<2时,f(x)min=f($\frac{a}{2}$)=-$\frac{{a}^{2}}{4}+a+1$;…(9分)
综上:f(x)min=$\left\{\begin{array}{l}{-\frac{{a}^{2}}{4}+a+1…a<2}\\{2…a≥2}\end{array}\right.$.…(10分)
点评 本题考查了用分类讨论处理分段函数的值域问题,属于中档题.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要的条件 | B. | 必要而不充分的条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要的条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)<f(2)<f(4) | B. | f(2)<f(1)<f(4) | C. | f(4)<f(2)<f(1) | D. | f(4)<f(1)<f(2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $10\sqrt{2}a$ | B. | 10a | C. | $(5+\sqrt{5})a$ | D. | $12\sqrt{2}a$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
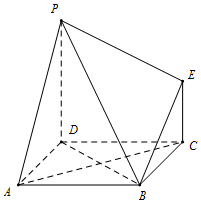 如图为一组合几何体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD且PD=AD=2EC=2.
如图为一组合几何体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD且PD=AD=2EC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com