
| A. | 充分而不必要的条件 | B. | 必要而不充分的条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要的条件 |
分析 由题意,可由函数的性质得出f(x)为[-1,0]上是减函数,再由函数的周期性即可得出f(x)为[3,4]上的减函数,由此证明充分性,再由f(x)为[3,4]上的减函数结合周期性即可得出f(x)为[-1,0]上是减函数,再由函数是偶函数即可得出f(x)为[0,1]上的增函数,由此证明必要性,即可得出正确选项
解答 解:∵f(x)是定义在R上的偶函数,
∴若f(x)为[0,1]上的增函数,则f(x)为[-1,0]上是减函数,
又∵f(x)是定义在R上的以2为周期的函数,且[3,4]与[-1,0]相差两个周期,
∴两区间上的单调性一致,所以可以得出f(x)为[3,4]上的减函数,故充分性成立.
若f(x)为[3,4]上的减函数,同样由函数周期性可得出f(x)为[-1,0]上是减函数,再由函数是偶函数可得出f(x)为[0,1]上的增函数,故必要性成立.
综上,“f(x)为[0,1]上的增函数”是“f(x)为[3,4]上的减函数”的充要条件.
故选C.
点评 本题考查充分性与必要性的判断,解题的关键是理解充分性与必要性证明的方向,即由那个条件到那个条件的证明是充分性,那个方向是必要性,初学者易搞不清证明的方向导致表述上出现逻辑错


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4) | B. | [1,2] | C. | [2,4] | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
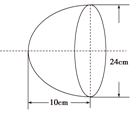 如图所示,汽车前反光镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反光镜的轴垂直,灯泡位于抛物线的焦点处,已知灯口的直径是24cm,灯深10cm.那么灯泡与反光镜的顶点(即截得抛物线的顶点)距离为( )
如图所示,汽车前反光镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反光镜的轴垂直,灯泡位于抛物线的焦点处,已知灯口的直径是24cm,灯深10cm.那么灯泡与反光镜的顶点(即截得抛物线的顶点)距离为( )| A. | 10 cm | B. | 7.2 cm | C. | 2.4 cm | D. | 3.6 cm |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
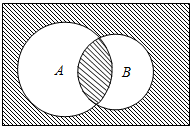
| A. | ∁UA∪(A∩B) | B. | ∁UA∩∁UB | C. | ∁UA∪∁UB | D. | ∁U(A∪B)∪(A∩B) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com