
科目:高中数学 来源: 题型:
若实数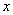 、
、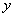 、
、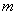 满足
满足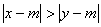 ,则称
,则称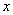 比
比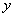 远离
远离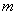 .
.
(1)若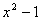 比
比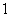 远离0,求
远离0,求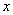 的取值范围;
的取值范围;
 (2)对于任意两个不相等的正数
(2)对于任意两个不相等的正数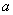 、
、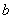 ,证明:
,证明: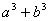 比
比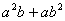 远离
远离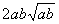 ;
;
(3)已知函数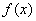 的定义域
的定义域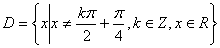 . 任取
. 任取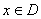 ,
,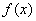 等于
等于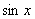 和
和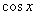 中远离0的那个值,写出函数
中远离0的那个值,写出函数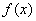 的解析式,并指出他的基本性质(结论不要求证明).
的解析式,并指出他的基本性质(结论不要求证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数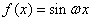
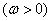 在区间
在区间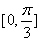 上单调递增,在区间
上单调递增,在区间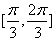 上单调递减;如图,四边形
上单调递减;如图,四边形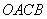 中,
中,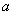 ,
,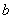 ,
,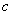 为
为 的内角
的内角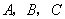 的对边,且满足
的对边,且满足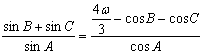 .
.
(Ⅰ)证明: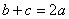 ;
;
(Ⅱ)若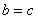 ,设
,设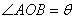 ,
,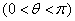 ,
,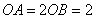 ,
,
求四边形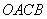 面积的最大值.
面积的最大值.
 |
查看答案和解析>>
科目:高中数学 来源: 题型:
某实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似满足函数关系:
f(t)=10-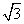 cos
cos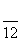 t-sin
t-sin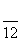 t,t∈[0,24).
t,t∈[0,24).
(1)求实验室这一天的最大温差.
(2)若要求实验室温度不高于11℃,则在哪段时间实验室需要降温?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com