
(本题满分13分)已知椭圆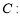
 的焦距为
的焦距为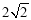 ,且过点
,且过点 .
.
(1)求椭圆的方程;
(2)已知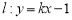 ,是否存在
,是否存在 使得点
使得点 关于
关于 的对称点
的对称点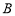 (不同于点
(不同于点 )在椭圆
)在椭圆 上?若存在求出此时直线
上?若存在求出此时直线 的方程,若不存在说明理由.
的方程,若不存在说明理由.
(1)椭圆的方程为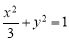 ;(2)不存在
;(2)不存在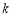 满足条件.
满足条件.
【解析】
试题分析:(1)由2c=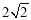 ,得
,得 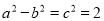 ;又点
;又点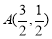 在椭圆
在椭圆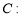
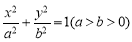 上,
上,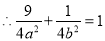 .解方程组求出
.解方程组求出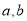 ,即可得椭圆的方程;(2)当
,即可得椭圆的方程;(2)当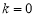 时,直线
时,直线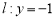 ,可求出点
,可求出点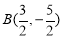 ,检验知,不在椭圆上;当
,检验知,不在椭圆上;当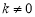 时,可设直线
时,可设直线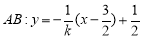 ,即
,即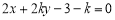 代入
代入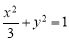 整理得
整理得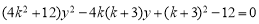 ,因为
,因为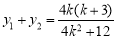 ,所以
,所以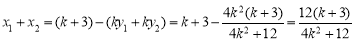 若
若 关于直线
关于直线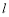 对称,则其中点
对称,则其中点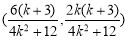 在直线
在直线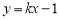 上.所以
上.所以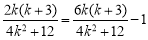 ,解得
,解得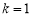 因为此时点
因为此时点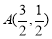 在直线
在直线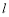 上,所以对称点
上,所以对称点 与点
与点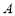 重合,不合题意所以不存在
重合,不合题意所以不存在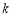 满足条件.
满足条件.
试题解析:(1)由已知,焦距为2c=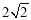 1分
1分
又 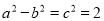 2分
2分
点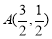 在椭圆
在椭圆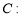
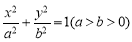 上,
上,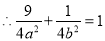 3分
3分
故,所求椭圆的方程为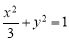 5分
5分
(2)当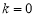 时,直线
时,直线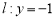 ,点
,点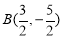 不在椭圆上; 7分
不在椭圆上; 7分
当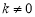 时,可设直线
时,可设直线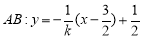 ,即
,即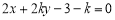 8分
8分
代入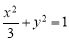 整理得
整理得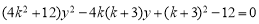
因为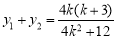 ,所以
,所以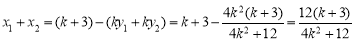
若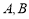 关于直线
关于直线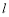 对称,则其中点
对称,则其中点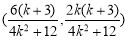 在直线
在直线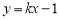 上 10分
上 10分
所以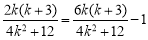 ,解得
,解得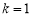 因为此时点
因为此时点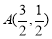 在直线
在直线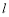 上, 12分
上, 12分
所以对称点 与点
与点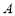 重合,不合题意所以不存在
重合,不合题意所以不存在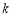 满足条件. 13分
满足条件. 13分
考点:1、椭圆的方程;2、直线与圆锥曲线的位置关系.


 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源:2014-2015学年山东省潍坊市高三上学期期中考试理科数学试卷(解析版) 题型:选择题
“直线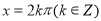 ”是“函数
”是“函数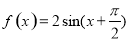 图象的对称轴”的( )
图象的对称轴”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省浏阳、醴陵、攸县三校高三联考文科数学试卷(解析版) 题型:选择题
已知函数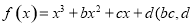 均为常数
均为常数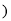 ,当
,当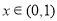 时取极大值,当
时取极大值,当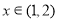 时取极小值,则
时取极小值,则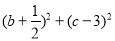 的取值范围是( )
的取值范围是( )
A.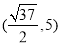 B.
B. C.
C. D.
D.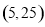
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省浏阳、醴陵、攸县三校高三联考理科数学试卷(解析版) 题型:填空题
设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2,若对任意x∈[a,a+2],不等式
f(x+a)≥f(3x+1)恒成立,则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省浏阳、醴陵、攸县三校高三联考理科数学试卷(解析版) 题型:选择题
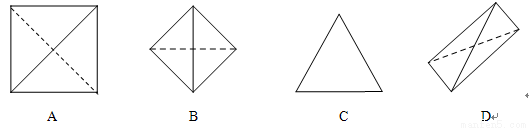
已知点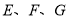 分别是正方体
分别是正方体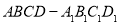 的棱
的棱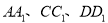 的中点,点
的中点,点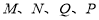 分别在线段
分别在线段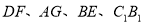 上.以
上.以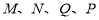 为顶点的三棱锥
为顶点的三棱锥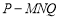 的俯视图不可能是( )
的俯视图不可能是( )

查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北省保定市高三上学期12月份联考文科数学试卷(解析版) 题型:选择题
已知函数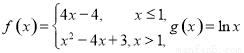 ,则函数
,则函数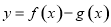 的零点个数为( )
的零点个数为( )
A.1 B. 2 C. 3 D.4
查看答案和解析>>
科目:高中数学 来源:2014-2015学年安徽省江淮名校高三第二次联考文科数学试卷(解析版) 题型:填空题
若正实数a使得不等式|2x - a|+|3x- 2a|≥a2对任意实数x恒成立,则实数a的范围是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com