
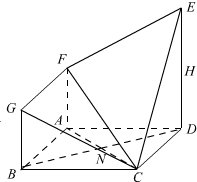
 在如图所示的几何体ABCDEFG中,四边形ABCD是边长为4的正方形,DE⊥平面ABCD,DE∥AF∥BG,H是DE的中点,AC与BD相交于N,DE=2AF=2BG=4
在如图所示的几何体ABCDEFG中,四边形ABCD是边长为4的正方形,DE⊥平面ABCD,DE∥AF∥BG,H是DE的中点,AC与BD相交于N,DE=2AF=2BG=4分析 (Ⅰ)P为FH的中点R,证明四边形MRNQ为平行四边形,可得MQ∥NR,即可证明NP∥平面EFC;
(Ⅱ)建立坐标系,求出平面GFC的法向量、平面EFC的法向量,即可求二面角E-FC-G的余弦值.
解答 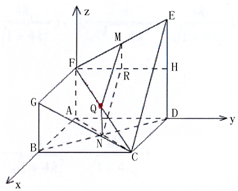 解:(Ⅰ)分别取EF、FH、CF的中点M、R、Q,连接MR、MQ、NQ、NR,
解:(Ⅰ)分别取EF、FH、CF的中点M、R、Q,连接MR、MQ、NQ、NR,
则MR∥EH∥FA∥NQ且MR=$\frac{1}{2}$EH=$\frac{1}{2}$FA=NQ
∴四边形MRNQ为平行四边形,
∴MQ∥NR
又MQ?平面EFC,NR?平面EFC,
∴NR∥平面EFC,即P为FH的中点R.…(5分)
(Ⅱ)分别以直线AB、AD、AF为x、y、z轴,建立空间直角坐标系,如图所示.
则G(4,0,2),F(0,0,2),C(4,4,0),E(0,4,4)
设平面GFC的法向量为$\overrightarrow{m}$=(x,y,z),$\overrightarrow{FG}$=(4,0,0),$\overrightarrow{CG}$=(0,-4,2)
则$\left\{\begin{array}{l}{x=0}\\{2y-z=0}\end{array}\right.$,令z=2得:$\overrightarrow{m}$=(0,1,2)
类似可得平面EFC的法向量为$\overrightarrow{n}$=(2,-1,2),
∴cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\sqrt{5}}{5}$,∴二面角E-FC-G的余弦值为-$\frac{\sqrt{5}}{5}$.…(12分)
点评 本题考查直线与平面平行的判定,二面角E-FC-G的余弦值、考查逻辑思维能力,空间想象能力,关键是求出平面的法向量.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1+\sqrt{3}}{4}i$ | B. | $\frac{1+\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}-1}{4}i$ | D. | $\frac{\sqrt{3}-1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com