
���� ��1����e=$\frac{1}{2}$�ɵã�a2=4c2���ٸ��������������ʽ�����Բ���̣�
��2��ֱ�ߺ���Բ���������飬�õ���P��������ֱ���ô�ֱ��ϵ�õ���Ӧ��ϵʽ���Ӷ���ʽ��⣮
��� �⣺��1����e=$\frac{1}{2}$�ɵã�a2=4c2����
${S}_{��{F}_{1}A{F}_{2}}=\frac{1}{2}|A{F}_{1}||A{F}_{2}|sin60��$�T$\sqrt{3}$���ɵã�|AF1||AF2|=4
�ڡ�F1AF2�������Ҷ����У�$|{F}_{1}A{|}^{2}+|{F}_{2}A{|}^{2}-2|{F}_{1}A||{F}_{2}A|cos60��$=4c2����|AF1|+|AF2|=2a
�ɵ�a2-c2=3��
�����٢ڵã�a2=4��c2=1����b2=3��
������Բ�ķ���Ϊ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$
��2�����P��x0��y0����$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$����
��4k2+3��x2+8kmx+4m2-12=0
��=64k2m2-4��4k2+3����4m2-12��=0�������4k2-m2+3=0��
��${x}_{0}=-\frac{4km}{4{k}^{2}+3}=-\frac{4k}{m}��{y}_{0}=\frac{3}{m}$
����P��$-\frac{4k}{m}��\frac{3}{m}$��
��$\left\{\begin{array}{l}{y=kx+m}\\{x=4}\end{array}\right.$����Q��4��4k+m����������ڵ�M������Ϊ��x1��0������$\overrightarrow{MP}=��-\frac{4k}{m}-{x}_{1}��\frac{3}{m}��$��
$\overrightarrow{MQ}=��4-{x}_{1}��4k+m��$����Ϊ��PQΪֱ����Բ�����M������$\overrightarrow{MP}•\overrightarrow{MQ}=0$����$-\frac{16k}{m}+\frac{4k{x}_{1}}{m}-4{x}_{1}+{x}_{1}^{2}+\frac{12k}{m}+3=0$
������$��4{x}_{1}-4��\frac{k}{m}+{x}_{1}^{2}-4{x}_{1}+3=0$�������k��m��������
��$\left\{\begin{array}{l}{4{x}_{1}-4=0}\\{{x}_{1}^{2}-4{x}_{1}+3=0}\end{array}\right.$���x1=1���ʴ��ڶ���M��1��0���������⣮
���� ������Ҫ��������Բ���̵�����ֱ����Բ���ߵ��ۺ����⣬���������ͣ�


 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д� �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|x��-$\frac{5}{4}$��x��2} | B�� | {x|x��-$\frac{5}{4}$} | C�� | {x|x��-$\frac{5}{4}$��x��-5} | D�� | {x|x��-$\frac{5}{4}$} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | Sn=$\frac{n��n-1��}{2}$ | B�� | Sn=$\frac{n��n+1��}{2}$ | C�� | Sn=2n-1 | D�� | Sn=2n-1-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
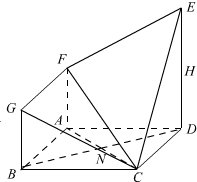 ����ͼ��ʾ�ļ�����ABCDEFG�У��ı���ABCD�DZ߳�Ϊ4�������Σ�DE��ƽ��ABCD��DE��AF��BG��H��DE���е㣬AC��BD�ཻ��N��DE=2AF=2BG=4
����ͼ��ʾ�ļ�����ABCDEFG�У��ı���ABCD�DZ߳�Ϊ4�������Σ�DE��ƽ��ABCD��DE��AF��BG��H��DE���е㣬AC��BD�ཻ��N��DE=2AF=2BG=4�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
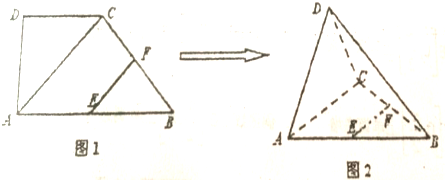
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com