
| A. | Sn=$\frac{n(n-1)}{2}$ | B. | Sn=$\frac{n(n+1)}{2}$ | C. | Sn=2n-1 | D. | Sn=2n-1-1 |
分析 根据解析式函数f(x)得出归纳推理得出f(n)=n,n∈N,得出g(x)的零点为:0,1,2,3,4…n-1,运用等差数列的知识求解即可.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-1(x≤0)}\\{f(x-1)+1(x>0)}\end{array}\right.$,
∴f(0)=0,f(1)=f(0)+1=1,f(2)=f(1)+1=2,
f(3)=f(2)+1=3,
归纳推理得出f(n)=n,n∈N
∵g(x)=f(x)-x,
∴g(x)的零点为:0,1,2,3,4…n-1,
∵函数g(x)的零点按从小到大的顺序排列成一个数列,
∴该数的前n项和为:$\frac{n(0+n-1)}{2}$=$\frac{n(n-1)}{2}$
故选:A
点评 本题考查了函数的性质,零点的问题,融合了数列的知识,综合性较强,难度较大,属于中档题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1+\sqrt{3}}{4}i$ | B. | $\frac{1+\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}-1}{4}i$ | D. | $\frac{\sqrt{3}-1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α⊥β,m∥α,则m⊥β | B. | 若m∥α,n∥m,则n∥α | ||
| C. | 若m∥α,n∥β,且m∥n,则α∥β | D. | 若m⊥β,m∥α,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
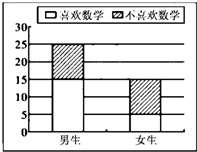 对某中学高二某班40名学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二堆条形图如图所示.
对某中学高二某班40名学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二堆条形图如图所示.| 喜欢数学课程 | 不喜欢数学课程 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 | 40 |
| P(K2≥k0) | 0.5 | 0.4 | 0.25 | 0.15 | 0.1 | 0.01 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com