
分析 分别画出两个区域对应的图形,求出面积,利用几何概型公式解答.根据二元一次不等式组表示的平面区域的原理,分别作出集合Ω和集合A对应的平面区域,得到它们都直角三角形.计算出这两个直角三角形的面积后,再用符合题的面积即小三角形面积,除以整个图形即大三角形的面积得到概率
解答  解:区域Ω是不等式组$\left\{\begin{array}{l}{x+y<6}\\{x>0}\\{y>0}\end{array}\right.$表示的平面区域如图三角形区域OEF,面积为$\frac{1}{2}×6×6=18$;
解:区域Ω是不等式组$\left\{\begin{array}{l}{x+y<6}\\{x>0}\\{y>0}\end{array}\right.$表示的平面区域如图三角形区域OEF,面积为$\frac{1}{2}×6×6=18$;
A是不等式组$\left\{\begin{array}{l}{x<4}\\{y>0}\\{x-2y>0}\end{array}\right.$表示的平面区域,如图阴影部分,面积为$\frac{1}{2}×4×2$=4,
由几何概型公式可得点P落入区域A的概率为:$\frac{4}{18}=\frac{2}{9}$;
故答案为:$\frac{2}{9}$.
点评 本题着重考查了二元一次不等式组表示的平面区域和几何概率模型.准确画作相应的平面区域,熟练地运用面积比求相应的概率,是解决本题的关键


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:选择题
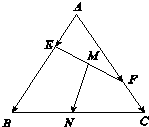 如图,在边长为1的正三角形ABC中,E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|$\overrightarrow{MN}$|的最小值为( )
如图,在边长为1的正三角形ABC中,E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|$\overrightarrow{MN}$|的最小值为( )| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>-$\frac{5}{4}$且x≠2} | B. | {x|x>-$\frac{5}{4}$} | C. | {x|x<-$\frac{5}{4}$且x≠-5} | D. | {x|x<-$\frac{5}{4}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点F是PD的中点,点E在CD上移动.
如图,在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点F是PD的中点,点E在CD上移动.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
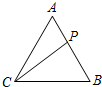 如图,在等边三角形ABC中,P在线段AB上,且$\overrightarrow{AP}=λ\overrightarrow{AB}$,其中0<λ<1,若$\overrightarrow{PA}•\overrightarrow{PB}+\overrightarrow{PC}•\overrightarrow{AB}$=0,则λ的值为$\frac{{2-\sqrt{2}}}{2}$.
如图,在等边三角形ABC中,P在线段AB上,且$\overrightarrow{AP}=λ\overrightarrow{AB}$,其中0<λ<1,若$\overrightarrow{PA}•\overrightarrow{PB}+\overrightarrow{PC}•\overrightarrow{AB}$=0,则λ的值为$\frac{{2-\sqrt{2}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | Sn=$\frac{n(n-1)}{2}$ | B. | Sn=$\frac{n(n+1)}{2}$ | C. | Sn=2n-1 | D. | Sn=2n-1-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com