
以直角坐标系的原点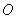 为极点,
为极点,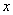 轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线
轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线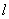 的参数方程为
的参数方程为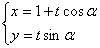 (
(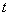 为参数,
为参数,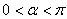 ),曲线
),曲线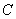 的极坐标方程为
的极坐标方程为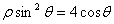 .
.
(Ⅰ)求曲线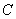 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线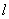 与曲线
与曲线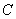 相交于
相交于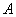 、
、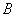 两点,当
两点,当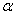 变化时,求
变化时,求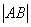 的最小值.
的最小值.
科目:高中数学 来源: 题型:
在平面直角坐标系中,设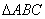 的顶点分别为
的顶点分别为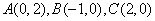 ,圆
,圆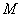 是
是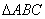 的外接圆,直线
的外接圆,直线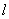 的方程是
的方程是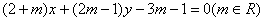
(1)求圆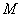 的方程;
的方程;
(2)证明:直线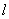 与圆
与圆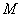 相交;
相交;
(3)若直线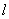 被圆
被圆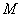 截得的弦长为3,求
截得的弦长为3,求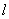 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
对于函数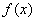 ,若存在
,若存在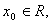 ,使
,使 成立,则称
成立,则称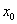 为
为 的“滞点”?已知函数
的“滞点”?已知函数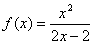 .
.
(1)试问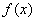 有无“滞点”?若有,求之,否则说明理由;
有无“滞点”?若有,求之,否则说明理由;
(2)已知数列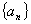 的各项均为负数,且满足
的各项均为负数,且满足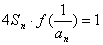 ,求数列
,求数列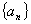 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
2014年我国公布了新的高考改革方案,在招生录取制度改革方面,普通高校逐步推行基于统一高考和高中学业水平考试成绩的综合评价、多元录取机制,普通高校招生录取将参考考生的高中学业水平考试成绩和职业倾向性测试成绩。
为了解公众对“改革方案”的态度,随机抽查了50人,将调查情况进行整理后制成下表:

(1)完成被调查人员的频率分布直方图;
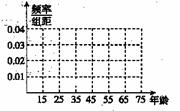 (2)若年龄在[15,25),[55,65)的被调查者中赞成人数分别为4人和3人,现从这两组的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“改革方案”的人数为X,求随机变量X的分布列和数学期望.
(2)若年龄在[15,25),[55,65)的被调查者中赞成人数分别为4人和3人,现从这两组的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“改革方案”的人数为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
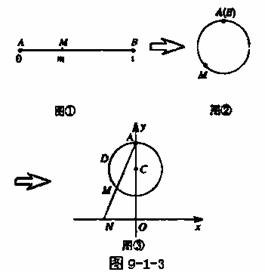
图9-1-3展示了一个由区间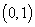 到实数集
到实数集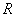 的映射过程:区间
的映射过程:区间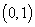 中的实数
中的实数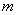 对应数轴上的点
对应数轴上的点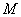 ,如图9-2中的图①;将线段
,如图9-2中的图①;将线段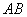 围成一个圆,使两端点
围成一个圆,使两端点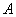 、
、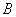 恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在
恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在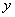 轴上,点
轴上,点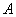 的坐标为
的坐标为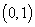 ,如图③.图③中直线
,如图③.图③中直线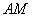 与
与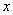 轴交于点
轴交于点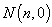 ,则
,则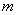 的象就是
的象就是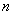 ,记作
,记作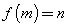 .
.
下列说法中正确命题的序号是 .(填出所有正确命题的序号)
①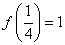 ; ②
; ②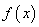 是奇函数;
是奇函数;
③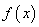 在定义域上单调递增; ④
在定义域上单调递增; ④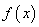 的图像关于点
的图像关于点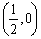 对称.
对称.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com