
分析 (1)函数f(x)=ax-a-x(其中0<a<1,x∈R)为奇函数,在R上且为减函数.运用奇偶性的定义和导数判断单调性,即可得证;
(2)由题意运用f(x)在R上为奇函数且为减函数,可得m<3x2-2x对0≤x≤1恒成立,由二次函数的最值求法,可得最小值,进而得到m的范围.
解答 解:(1)函数f(x)=ax-a-x(其中0<a<1,x∈R)为奇函数,
在R上且为减函数.
证明:定义域为R,f(-x)=a-x-ax=-f(x),
即有f(x)为奇函数;
由f(x)的导数为f′(x)=axlna+a-xlna=lna(ax+a-x),
由0<a<1可得lna<0,ax+a-x>0,即有f′(x)<0,
则f(x)在R上递减;
(2)若f(-2x2+3x)+f(m-x-x2)>0对任意的x∈[0,1]均成立,
即为f(-2x2+3x)>-f(m-x-x2)=f(x2+x-m),
由f(x)为R上的减函数,可得
-2x2+3x<x2+x-m,对0≤x≤1恒成立,
即有m<3x2-2x对0≤x≤1恒成立,
由y=3x2-2x在x=$\frac{1}{3}$处取得最小值,且为-$\frac{1}{3}$,
则m<-$\frac{1}{3}$,即有实数m的取值范围是(-∞,-$\frac{1}{3}$).
点评 本题考查函数的奇偶性和单调性的判断和运用,考查指数函数的单调性,同时考查不等式恒成立问题的解法,注意运用参数分离和二次函数的最值的求法,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | “0<x<$\frac{1}{2}$”是“x(1-2x)>0”的必要不充分条件 | |
| C. | 命题“?x0∈R,使得x02+x0+1<0”的否定是:“?x∈R,均有x2+x+1>0” | |
| D. | 命题“在△ABC中,若A>B,则sinA>sinB”的逆否命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
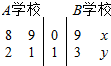 以下茎叶图记录了在高三一诊模拟考试中,A,B两个学校的各4个班的优生人数,其中有两个数据模糊不清,在图中用x,y表示,统计显示,A,B两个学校的优生人数的平均值相等,A校优生人数的方差比B校优生人数的方差小1.
以下茎叶图记录了在高三一诊模拟考试中,A,B两个学校的各4个班的优生人数,其中有两个数据模糊不清,在图中用x,y表示,统计显示,A,B两个学校的优生人数的平均值相等,A校优生人数的方差比B校优生人数的方差小1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,-1,2) | B. | (-4,-1,2) | C. | (-4,1,2) | D. | (4,-1,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com