Question

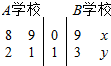
7．以下茎叶图记录了在高三一诊模拟考试中，A，B两个学校的各4个班的优生人数，其中有两个数据模糊不清，在图中用x，y表示，统计显示，A，B两个学校的优生人数的平均值相等，A校优生人数的方差比B校优生人数的方差小1．
（Ⅰ）求实数x，y的值；
（Ⅱ）从A，B两校中各随机抽取一个班级，记这两个班的优生人数分别为m，n，求随机变量ξ=|m-n|的分布列及数学期望．

Answer 1

分析 （Ⅰ）由茎叶图先求出A学校每个班优生人数的平均值和方差，由A，B两个学校的优生人数的平均值相等，A校优生人数的方差比B校优生人数的方差小1，列出方程组能求出x，y．
（Ⅱ）由已知得ξ可能取值为0，1，2，3，4，5，分别求出相应的概率，由此能求出ξ的分布列与Eξ．

解答 解：（Ⅰ）由茎叶图得A学校每个班优生人数的平均值为：$\overline{{x}_{A}}$=$\frac{1}{4}（8+9+11+12）$=10，
A校优生人数的方差为：${{S}_{A}}^{2}=\frac{1}{4}$[（8-10）²+（9-10）²+（11-10）²+（12-10）²]=2.5，
∵A，B两个学校的优生人数的平均值相等，A校优生人数的方差比B校优生人数的方差小1，
∴$\left\{\begin{array}{l}{\overline{{x}_{B}}=\frac{1}{4}（9+x+13+10+y）=10}\\{{{S}_{B}}^{2}=\frac{1}{4}[（9-10）^{2}+（x-10）^{2}+（13-10）^{2}+{y}^{2}=2.5+1}\end{array}\right.$，
解得x=8，y=0．
（Ⅱ）由已知得ξ可能取值为0，1，2，3，4，5，
P（ξ=0）=$\frac{1}{4}×\frac{1}{4}+\frac{1}{4}×\frac{1}{4}$=$\frac{2}{16}$=$\frac{1}{8}$，
P（ξ=1）=$\frac{1}{4}×\frac{1}{4}+\frac{1}{4}×\frac{2}{4}+\frac{1}{4}×\frac{1}{4}+\frac{1}{4}×\frac{1}{4}$=$\frac{5}{16}$，
P（ξ=2）=$\frac{1}{4}×\frac{1}{4}+\frac{1}{4}×\frac{2}{4}+\frac{1}{4}×\frac{1}{4}$=$\frac{4}{16}$=$\frac{1}{4}$，
P（ξ=3）=$\frac{1}{4}×\frac{1}{4}$=$\frac{1}{16}$，
P（ξ=4）=$\frac{1}{4}×\frac{1}{4}+\frac{1}{4}×\frac{1}{4}$=$\frac{2}{16}=\frac{1}{8}$，
P（ξ=5）=$\frac{1}{4}×\frac{1}{4}$=$\frac{1}{16}$，
∴ξ的分布列为：

ξ	0	1	2	3	4	5
P	$\frac{1}{8}$	$\frac{5}{16}$	$\frac{1}{4}$	$\frac{1}{16}$	$\frac{1}{8}$	$\frac{1}{16}$

Eξ=$0×\frac{1}{8}+1×\frac{5}{16}+2×\frac{1}{4}+3×\frac{1}{16}+4×\frac{1}{8}$+5×$\frac{1}{16}$=$\frac{29}{16}$．

点评 本题考查茎叶图的应用，考查离散型随机变量的分布列和数学期望的求法，是中档题，解题时要认真审题，在历年高考中都是必考题型之一．