
分析 ①根据向量平行的坐标公式进行求解判断.
②根据角的终边的性质进行判断.
③根据抽象函数的定义和奇偶性的定义进行判断.
④根据三角函数的性质进行判断.
⑤根据平面向量的基本定理进行判断.
解答 解:①若$\overrightarrow{a}$=(1,k),$\overrightarrow{b}$=(-2,6),$\overrightarrow{a}$∥$\overrightarrow{b}$,则-2k-6=0得k=-3,故①正确;
②终边在y轴上的角的集合是{α|α=kπ+$\frac{π}{2}$,k∈Z},故②错误;
③令a=2,b=1,则f(2)=f(2)+f(1),解得f(1)=0,
令a=-1,b=-1,则f(1)=f(-1)+f(-1)=2f(-1)=0,则f(-1)=0,
令b=-1,代入上式,
∴f(-a)=f(-1)+f(a)=f(a),
∴f(x)是偶函数.故③正确;
④函数y=sin(x-$\frac{π}{2}$)=-cosx在[0,π]上是增函数,故④错误;
⑤由已知条件知:${\overrightarrow{OC}}^{2}=1=(x\overrightarrow{OA}+y\overrightarrow{OB})^{2}$=${x}^{2}{\overrightarrow{OA}}^{2}+2xy\overrightarrow{OA}•\overrightarrow{OB}+{y}^{2}{\overrightarrow{OB}}^{2}$=x2-xy+y2=(x+y)2-3xy;
∴(x+y)2-1=3xy,根据向量加法的平行四边形法则,容易判断出x,y>0,
∴$x+y≥2\sqrt{xy}$,∴$xy≤\frac{(x+y)^{2}}{4}$;
∴$(x+y)^{2}-1≤\frac{3}{4}(x+y)^{2}$,∴(x+y)2≤4,∴x+y≤2,即x+y的最大值为2.故⑤正确,
故答案为:①③⑤
点评 本题主要考查命题的真假判断,涉及平面向量的基本内容以及三角函数,函数奇偶性的判断,涉及的知识点较多,综合性较强.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2x | B. | y=4x | C. | y=$\frac{1}{2}$x | D. | y=$\frac{1}{4}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,+∞) | B. | (-2,-$\frac{1}{2}$) | C. | (-∞,-$\frac{1}{2}$) | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
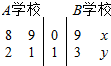 以下茎叶图记录了在高三一诊模拟考试中,A,B两个学校的各4个班的优生人数,其中有两个数据模糊不清,在图中用x,y表示,统计显示,A,B两个学校的优生人数的平均值相等,A校优生人数的方差比B校优生人数的方差小1.
以下茎叶图记录了在高三一诊模拟考试中,A,B两个学校的各4个班的优生人数,其中有两个数据模糊不清,在图中用x,y表示,统计显示,A,B两个学校的优生人数的平均值相等,A校优生人数的方差比B校优生人数的方差小1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com