
分析 (1)根据等值域变换的定义,分别进行推导判断即可.
(2)利用f(x)的定义域,求得值域,根据x的表达式,和t值域建立不等式,利用存在t1,t2∈R使两个等号分别成立,求得m和n.
解答 解:1°f(x)=x2-x+1=(x-$\frac{1}{2}$)2+$\frac{3}{4}$≥$\frac{3}{4}$,即函数f(x)的值域为[$\frac{3}{4}$,+∞),
①C=(1,+∞)时,g(t)∈(0,+∞),f(g(t))=(g(t))2-g(t)+1=(g(t)-$\frac{1}{2}$)2+$\frac{3}{4}$≥$\frac{3}{4}$,
即函数f(g(t))的值域为[$\frac{3}{4}$,+∞),即x=g(t)是函数y=f(x)的一个等值域变换
②B=R,C=(2,+∞)时,g(t)∈(1,+∞),f(g(t))=(g(t))2-g(t)+1=(g(t)-$\frac{1}{2}$)2+$\frac{3}{4}$>1′,
即函数f(g(t))的值域为(1,+∞),即x=g(t)不是函数y=f(x)的一个等值域变换,
故①是等值域变换,②不等值域变换
2°B=[0,4],C=[a,b](0<a<b),f(x)的值域为[$\frac{3}{4}$,13],x=g(t)的值域是[log2a,log2b]
当f(x)=13时,x=-3或4,结合图象可知,若x=g(t)是函数y=f(x)的一个等值域变换,
则$\left\{\begin{array}{l}{lo{g}_{2}a=-3}\\{\frac{1}{2}≤lo{g}_{2}b≤4}\end{array}\right.$或$\left\{\begin{array}{l}{lo{g}_{2}b=4}\\{-3<lo{g}_{2}a≤\frac{1}{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{1}{8}}\\{\sqrt{2}≤b≤16}\end{array}\right.$或$\left\{\begin{array}{l}{b=16}\\{\frac{1}{8}<a≤\sqrt{2}}\end{array}\right.$,
故若x=g(t)是函数y=f(x)的一个等值域变换,则a,b满足的条件是:
$\left\{\begin{array}{l}{a=\frac{1}{8}}\\{\sqrt{2}≤b≤16}\end{array}\right.$或$\left\{\begin{array}{l}{b=16}\\{\frac{1}{8}<a≤\sqrt{2}}\end{array}\right.$.
(2)f(x)=log2x定义域为[2,8],由y=log2x,知1≤y≤3,
即f(x)=log2x的值域为[1,3],
因为x=g(t)是y=f(x)的一个等值域变换,且函数f(g(t))的定义域为R,
所以x=g(t)=$\frac{m{t}^{2}-3t+n}{{t}^{2}+1}$,t∈R的值域为[2,8],
则2≤$\frac{m{t}^{2}-3t+n}{{t}^{2}+1}$≤8,
∴2(t2+1)≤mt2-3t+n≤8(t2+1),
所以,恒有$\left\{\begin{array}{l}{(m-2){t}^{2}-3t+n-2≥0}\\{(m-8){t}^{2}-3t+n-8≤0}\end{array}\right.$,
且存在t1,t2∈R使两个等号分别成立,
于是$\left\{\begin{array}{l}{2<m<8}\\{{△}_{1}=9-4(m-2)(n-2)=0}\\{{△}_{2}=9-4(m-8)(n-8)=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=5+\frac{3\sqrt{3}}{2}}\\{n=5-\frac{3\sqrt{3}}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{m=5-\frac{3\sqrt{3}}{2}}\\{n=5+\frac{3\sqrt{3}}{2}}\end{array}\right.$.
点评 本题主要考查了新定义的理解和运用,主要函数值域的问题,利用已知条件演绎推理的能力和运算能力.综合性较强,难度较大.


科目:高中数学 来源: 题型:选择题
| A. | 有两个面平行,其余各面都是平行四边形的几何体叫棱柱 | |
| B. | 有一个面是多边形,其余各面都是三角形的几何体叫棱锥 | |
| C. | 由五个面围成的多面体一定是四棱锥 | |
| D. | 棱台各侧棱的延长线交于一点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
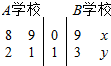 以下茎叶图记录了在高三一诊模拟考试中,A,B两个学校的各4个班的优生人数,其中有两个数据模糊不清,在图中用x,y表示,统计显示,A,B两个学校的优生人数的平均值相等,A校优生人数的方差比B校优生人数的方差小1.
以下茎叶图记录了在高三一诊模拟考试中,A,B两个学校的各4个班的优生人数,其中有两个数据模糊不清,在图中用x,y表示,统计显示,A,B两个学校的优生人数的平均值相等,A校优生人数的方差比B校优生人数的方差小1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-1,0)∪(1,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1)∪(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{7}{10}$ | B. | $\frac{7}{10}$ | C. | -7 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com