
【题目】高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
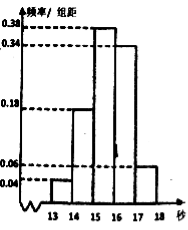
(1)请根据频率分布直方图估计该组数据的众数和中位数(精确到0.1);
(2)从成绩介于![]() 和
和![]() 两组的人中任取2人,求两人分布来自不同组的概率.
两组的人中任取2人,求两人分布来自不同组的概率.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:对问题(1),根据频率分布直方图的特征以及一组数据的众数就是频率分布直方图中最高矩形中点的横坐标,而中位数对应的直线将频率分布直方图的面积平分,进而可求出该组数据的中位数;对问题(2),首先求出成绩介于![]() 和
和![]() 的人数,再根据古典概型,即可求出两人分布来自不同组的概率.
的人数,再根据古典概型,即可求出两人分布来自不同组的概率.
试题解析:(1)由图可知众数落在第三组![]() 是
是![]() ...............2分
...............2分
因为数据落在第一、二组的频率![]() ,
,
数据落在第一、二、三组的频率![]() ,
,
所以中位数一定落在第三组![]() 中,假设中位数是
中,假设中位数是![]() ,所以
,所以![]() 解得中位数
解得中位数![]() ........................4分
........................4分
(2)由题意,![]() 组有
组有![]() 人,
人,![]() 组有
组有![]() 人;....................6分
人;....................6分
设![]() 组中
组中![]() 人分别为
人分别为![]() ;
;![]() 组中
组中![]() 人分别为
人分别为![]() ,事件
,事件![]() 为抽取的两人来自不同组,则基本事件有:
为抽取的两人来自不同组,则基本事件有:![]() 共
共![]() 种;
种;
事件![]() 包含基本事件有
包含基本事件有![]() 共
共![]() 种..................8分
种..................8分
所以![]() ...........................10分
...........................10分


科目:高中数学 来源: 题型:
【题目】设不等式组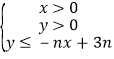 所表示的平面区域为
所表示的平面区域为![]() ,记
,记![]() 内的整点个数为
内的整点个数为![]() ,(整点即横、纵坐标均为整数的点)
,(整点即横、纵坐标均为整数的点)
(1)计算![]() 的值;
的值;
(2)求数列![]() 的通项公式
的通项公式![]() ;
;
(3)记数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,若对于一切的正整数
,若对于一切的正整数![]() ,总有
,总有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的焦点在
的焦点在![]() 轴上.
轴上.
(1)若椭圆![]() 的焦距为1,求椭圆
的焦距为1,求椭圆![]() 的方程;
的方程;
(2)设![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为椭圆
为椭圆![]() 上第一象限内的点,直线
上第一象限内的点,直线![]() 交
交![]() 轴于点
轴于点![]() ,并且
,并且![]() .证明:当
.证明:当![]() 变化时,点
变化时,点![]() 在定直线
在定直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别为椭圆
分别为椭圆![]() 左、右焦点,点
左、右焦点,点![]() 在椭圆上,且
在椭圆上,且![]() 轴,
轴,![]() 的周长为6.
的周长为6.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)![]() 是椭圆
是椭圆![]() 上异于点
上异于点![]() 的两个动点,如果直线
的两个动点,如果直线![]() 与直线
与直线![]() 的倾斜角互补,证明:直线
的倾斜角互补,证明:直线![]() 的斜率为定值,并求出这个定值.
的斜率为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒, 以防止害虫的危害, 但采集上市时蔬菜仍存有少量的残留农药, 食用时需要用清水清洗干净, 下表是用清水![]() (单位:千克) 清洗该蔬菜
(单位:千克) 清洗该蔬菜![]() 千克后, 蔬菜上残留的农药
千克后, 蔬菜上残留的农药![]() (单位:微克) 的统计表:
(单位:微克) 的统计表:
|
|
|
|
|
|
|
|
|
|
|
|
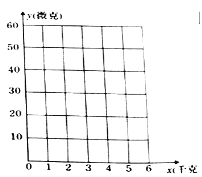
(1)在下面的坐标系中, 描出散点图, 并判断变量![]() 与
与![]() 的相关性;
的相关性;
(2)若用解析式![]() 作为蔬菜农药残量
作为蔬菜农药残量![]() 与用水量
与用水量![]() 的回归方程, 令
的回归方程, 令![]() ,计算平均值
,计算平均值![]() 与
与![]() ,完成以下表格(填在答题卡中) ,求出
,完成以下表格(填在答题卡中) ,求出![]() 与
与![]() 的回归方程.(
的回归方程.(![]() 精确到
精确到![]() )
)
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
(3)对于某种残留在蔬菜上的农药,当它的残留量低于![]() 微克时对人体无害, 为了放心食用该蔬菜, 请
微克时对人体无害, 为了放心食用该蔬菜, 请
估计需要用多少千克的清水清洗一千克蔬菜?(精确到![]() ,参考数据
,参考数据![]() )
)
(附:线性回归方程![]() 中系数计算公式分别为;
中系数计算公式分别为;
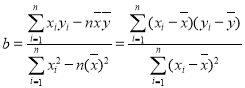 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个铝合金窗分为上、下两栏,四周框架和中间隔档的材料为铝合金,宽均为6![]() ,上栏与下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800
,上栏与下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800![]() ,设该铝合金窗的宽和高分别为
,设该铝合金窗的宽和高分别为![]() ,铝合金窗的透光部分的面积为
,铝合金窗的透光部分的面积为![]() .
.
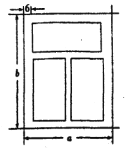
(1)试用![]() 表示
表示![]() ;
;
(2)若要使![]() 最大,则铝合金窗的宽和高分别为多少?
最大,则铝合金窗的宽和高分别为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )的图象与直线
)的图象与直线![]() (
(![]() )相切,并且切点横坐标依次成公差为
)相切,并且切点横坐标依次成公差为![]() 的等差数列,且
的等差数列,且![]() 的最大值为1.
的最大值为1.
(1)![]() ,求函数
,求函数![]() 的单调递增区间;
的单调递增区间;
(2)将![]() 的图象向左平移
的图象向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,若函数
的图象,若函数![]() 在
在![]() 上有零点,求实数
上有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com