【题目】已知函数
.
（1）若
，且函数
在其定义域内为增函数，求实数
的取值范围；
（2）设函数
，若在
上至少存在一点
，使得
成立，求实数的取值范围.
【答案】（1）
（2）
【解析】
（1）
＝
，求其导函数，利用F（x）在定义域（0，+∞）内为增函数，得
≥0在（0，+∞）上恒成立，得
，设
，利用导数求
最大值可得正实数p的取值范围；
（2）设函数
＝f（x）﹣g（x）＝px﹣
，x∈[1，e]，转化为 在[1，e]上至少存在一点x0，使得
求函数的导函数，然后对p分类求 的最大值即可.
（1）
，
.
由定义域
内为增函数，所以
在上恒成立，
所以
即，对任意
恒成立，
设，
=0的根为x=1
得在
上单调递增，在
上单调递减，
则
，所以
，即
.
（2）设函数
，
，
因为在
上至少存在一点
，使得
成立，则
，
①当
时，
，则在上单调递增，
，舍；
②当
时，
，
∵，∴
，
，
，则
，舍；
③当
时，
，
则在上单调递增，
，得
，
综上，
.
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】某地区2007年至2013年农村居民家庭纯收入y（单位：千元）的数据如下表：
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
（1）求y关于t的线性回归方程；
（2）利用（1）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入.
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
，
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，且满足bcosA﹣
asinB＝0．
（1）求A；
（2）已知a＝2，B＝
，求△ABC的面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在某校组织的高二女子排球比赛中，有
、
两个球队进入决赛，决赛采用7局4胜制．假设、两队在每场比赛中获胜的概率都是
．并记需要比赛的场数为
．
（Ⅰ）求大于4的概率；
（Ⅱ）求的分布列与数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】以下四个关于圆锥曲线的命题：
①设A，B是两个定点，
为非零常数，若
，则P的轨迹是双曲线；
②过定圆C上一定点A作圆的弦AB，O为原点，若向量
．则动点P的轨迹是椭圆；
③方程
的两根可以分别作为椭圆和双曲线的离心率；
④双曲线
与椭圆
有相同的焦点．
其中正确命题的序号为________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出下列三种说法：
①命题p：x0∈R，tan x0＝1，命题q：x∈R，x2－x＋1>0，则命题“p∧(
)”是假命题．
②已知直线l1：ax＋3y－1＝0，l2：x＋by＋1＝0，则l1⊥l2的充要条件是
＝－3.
③命题“若x2－3x＋2＝0，则x＝1”的逆否命题为“若x≠1，则x2－3x＋2≠0”．
其中所有正确说法的序号为________________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】港珠澳大桥是中国建设史上里程最长，投资最多，难度最大的跨海桥梁项目，大桥建设需要许多桥梁构件。从某企业生产的桥梁构件中抽取
件，测量这些桥梁构件的质量指标值，由测量结果得到如图所示的频率分布直方图，质量指标值落在区间
，
，
内的频率之比为
.
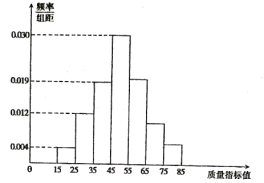
（1）求这些桥梁构件质量指标值落在区间内的频率；
（2）用分层抽样的方法在区间
内抽取一个容量为
的样本，将该样本看成一个总体，从中任意抽取
件桥梁构件，求这件桥梁构件都在区间
内的概率
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
：
，
为坐标原点，
为椭圆的左焦点，离心率为
，直线
与椭圆相交于
，
两点.
（1）求椭圆的方程；
（2）若
是弦
的中点，
是椭圆上一点，求
的面积最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
