
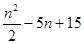 克,这些球等可能地从袋中被取出.
克,这些球等可能地从袋中被取出.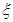 ,求E
,求E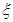 .
. ;(2)
;(2)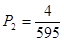 ;(3)E
;(3)E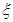 .=1
.=1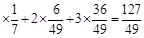 .
. 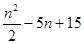 >n
>n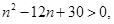 ……………………1分
……………………1分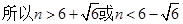 ,
,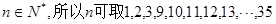 共30个数,…………3分
共30个数,…………3分 , ……………………4分
, ……………………4分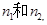
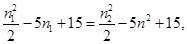
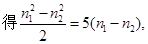 ………5分
………5分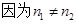 所以
所以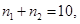
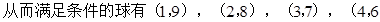 )…………7分
)…………7分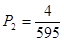 …………………………………8分
…………………………………8分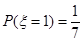
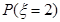 =
=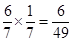 ;
;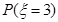 =
= ;
; 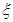 .=1
.=1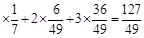 . ……………………12分
. ……………………12分

科目:高中数学 来源:不详 题型:解答题
 为取出的3枝里一等品的枝数,求
为取出的3枝里一等品的枝数,求 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 表示该同学猜灯谜结束后所得奖品的总金额。
表示该同学猜灯谜结束后所得奖品的总金额。 的数学期望
的数学期望 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 后放入乙盒,再从乙盒中任取一小球,记下号码
后放入乙盒,再从乙盒中任取一小球,记下号码 .
.  的概率;
的概率; ,求随机变量
,求随机变量 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
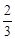 ,则该学生在面试时得分的期望值为 分.
,则该学生在面试时得分的期望值为 分.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
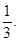 则这位司机在途中遇到红灯数ξ的方差为 . (用分数表示)
则这位司机在途中遇到红灯数ξ的方差为 . (用分数表示) 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
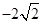 、
、 、
、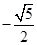 、0、
、0、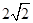 、
、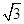 、
、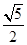 ,用ξ表示坐标原点到直线l的距离,则随机变量ξ的数学期望Eξ=_________.
,用ξ表示坐标原点到直线l的距离,则随机变量ξ的数学期望Eξ=_________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com