练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．已知随机变量X服从正态分布N（μ，σ2），且P（μ-2σ＜X＜μ+2σ）=0.954 4，P（μ-σ＜X＜μ+σ）=0.6826．若μ=4，σ=1，则P（5＜X＜6）=（　　）
    A．0.1359B．0.1358C．0.2718D．0.2716

    分析 根据变量符合正态分布，和所给的μ和σ的值，根据3σ原则，得到P（2＜X≤6）=0.9544，P（3＜X≤5）=0.6826，两个式子相减，根据对称性得到结果．

    解答 解：∵随机变量X服从正态分布N（μ，σ2），P（μ-2σ＜X≤μ+2σ）=0.9544，P（μ-σ＜X≤μ+σ）=0.6826，μ=4，σ=1，
    ∴P（2＜X≤6）=0.9544，P（3＜X≤5）=0.6826，
    ∴P（2＜X≤6-P（3＜X≤5）=0.9544-0.6826=0.2718，
    ∴P（5＜X＜6）=$\frac{1}{2}$×0.2718=0.1359
    故选：A．

    点评 本题考查正态分布曲线的特点及曲线所表示的意义，考查正态分布中两个量μ和σ的应用，考查曲线的对称性，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    13．设函数f（x）=x-alnx+$\frac{1-a}{x}$．
    （Ⅰ）若a＞1，求函数f（x）的单调区间；
    （Ⅱ）若a＞3，函数g（x）=a2x2+3，若存在x1，x2∈[$\frac{1}{2}$，2]，使得|f（x1）-g（x2）|＜9成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．如图，在四棱锥A-BCDE中，平面ABC⊥平面BCDE，∠CDE=∠BED=90°，AB=CD=2，DE=BE=1，$AC=\sqrt{2}$，F为AD的中点．
    （Ⅰ）求证：EF∥平面ABC；
    （Ⅱ）求证：AC⊥平面BCDE；
    （Ⅲ）求直线AE与平面ABC所成角的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．曲线f（x）=x2+x在（1，f（1））处的切线方程为（　　）
    A．2x-y-1=0B．2x-y=0C．3x-y+1=0D．3x-y-1=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．f（x）=Asin（ωx+φ）（A，ω＞0）部分图象如图，则函数表达式为f（x）=$\sqrt{2}$sin（2x+$\frac{π}{3}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知f′（x）是定义在R上的函数f（x）的导函数，且f（x）+f′（x）＞0，则a=2f（ln2），b=ef（1），c=f（0）的大小关系为（　　）
    A．a＜b＜cB．b＜a＜cC．c＜a＜bD．c＜b＜a

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．tan330°的值为（　　）
    A．-$\frac{\sqrt{3}}{3}$B．$\frac{\sqrt{3}}{3}$C．$\sqrt{3}$D．-$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．等差数列{an}的公差为2，若a1+a3+a5=3，则a4+a6+a8=（　　）
    A．30B．21C．18D．15

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

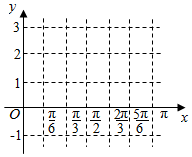    13．设函数f（x）=1+cos2x+$\sqrt{3}$sin2x
    （1）若函数f（x）=1-$\sqrt{3}$，且x∈[-$\frac{π}{3}$，$\frac{π}{3}$]，求x；
    （2）求函数y=f（x）的单调增区间，并在给出的坐标系中画出y=f（x）在区间[0，π]上的图象．

    查看答案和解析>>

    同步练习册答案