
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | c<b<a |
分析 构造函数g(x)=f(x)•ex,利用导数可判断g(x)的单调性,由单调性可得a=g(ln2)与c=g(0)、b=g(1)的大小关系,即可得到答案.
解答 解:令g(x)=f(x)•ex,
则g′(x)=f′(x)•ex+f(x)•ex=ex•(f(x)+f′(x)),
因为对任意x∈R都有f′(x)+f(x)>0,
所以g′(x)>0,即g(x)在R上单调递增,
又a=2f(ln2)=eln2f(ln2)=g(ln2),b=ef(1)=g(1),c=e0f(0)=g(0),
由0<ln2<1,可得g(0)<g(ln2)<g(1),
即c<a<b.
故选:C.
点评 本题考查导数的运用:求单调性,考查导数的运算性质的运用,以及单调性的运用:比较大小,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
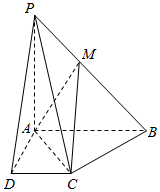 如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2.
如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $2\sqrt{3}$ | C. | $2\sqrt{6}$ | D. | $\frac{{7\sqrt{6}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.1359 | B. | 0.1358 | C. | 0.2718 | D. | 0.2716 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 8 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com