
 如图,点C在以AB为直径的圆O上,PA垂直于圆O所在的平面,G为△AOC的重心.
如图,点C在以AB为直径的圆O上,PA垂直于圆O所在的平面,G为△AOC的重心.分析 (1)延长OG交AC于点M.可得OM∥BC.由AB是圆O的直径,得OM⊥AC.
由PA⊥平面ABC,可得OM⊥平面PAC.即OG⊥平面PAC,证得平面OPG⊥平面PAC.
(2)以点C为原点,$\overrightarrow{CB},\overrightarrow{CA},\overrightarrow{AP}$方向分别为x,y,z轴正方向建立空间直角坐标系Cxyz,则C(0,0,0),$A({0,1,0}),B({\sqrt{3},0,0}),O({\frac{{\sqrt{3}}}{2},\frac{1}{2},0}),P({0,1,2}),M({0,\frac{1}{2},0})$
利用向量法求解.
解答 解:(1)证明:如图,延长OG交AC于点M.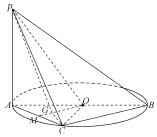
因为G为△AOC的重心,所以M为AC的中点.
因为O为AB的中点,所以OM∥BC.
因为AB是圆O的直径,所以BC⊥AC,所以OM⊥AC.
因为PA⊥平面ABC,OM?平面ABC,所以PA⊥OM.
又PA?平面PAC,AC?平面PAC,PA∩AC=A,所以OM⊥平面PAC.
即OG⊥平面PAC,又OG?平面OPG,
所以平面OPG⊥平面PAC.
(2)解:以点C为原点,$\overrightarrow{CB},\overrightarrow{CA},\overrightarrow{AP}$方向分别为x,y,z轴正方向建立空间直角坐标系Cxyz,
则C(0,0,0),$A({0,1,0}),B({\sqrt{3},0,0}),O({\frac{{\sqrt{3}}}{2},\frac{1}{2},0}),P({0,1,2}),M({0,\frac{1}{2},0})$,
则$\overrightarrow{OM}=({-\frac{{\sqrt{3}}}{2},0,0}),\overrightarrow{OP}=({-\frac{{\sqrt{3}}}{2},\frac{1}{2},2})$.
平面OPG即为平面OPM,设平面OPM的一个法向量$\overrightarrow n=({x,y,z})$,
则$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{OM}=-\frac{{\sqrt{3}}}{2}x=0\\ \overrightarrow n•\overrightarrow{OP}=-\frac{{\sqrt{3}}}{2}x+\frac{1}{2}y+2z=0\end{array}\right.$
令z=1,得$\overrightarrow n=({0,-4,1})$.
过点C作CH⊥AB于点H,由PA⊥平面ABC,
易得CH⊥PA,又PA∩AB=A,所以CH⊥平面PAB,即CH为平面PAO的一个法向量.
在Rt△ABC中,由AB=2AC,得∠ABC=30°,则$∠HCB=60°,CH=\frac{1}{2}CB=\frac{{\sqrt{3}}}{2}$.
所以${x_H}=CHcos∠HCB=\frac{{\sqrt{3}}}{4},{y_H}=CHsin∠HCB=\frac{3}{4}$,
所以$\overrightarrow{CH}=({\frac{{\sqrt{3}}}{4},\frac{3}{4},0})$.
设二面角A-OP-G的大小为θ,
则$cosθ=\frac{{|{\overrightarrow{CH}•\overrightarrow n}|}}{{|{\overrightarrow{CH}}|•|{\overrightarrow n}|}}=\frac{{|{0×\frac{{\sqrt{3}}}{4}+4×\frac{3}{4}+1×0}|}}{{\sqrt{\frac{3}{16}+\frac{9}{16}×\sqrt{{4^2}+{1^2}}}}}=\frac{{2\sqrt{51}}}{17}$
即二面角A-OP-G的余弦值为$\frac{{2\sqrt{51}}}{17}$.
点评 本题考查了空间面面垂直的判定,向量法求二面角,考查了转化思想、计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,-1,1,2} | B. | {-1,1} | C. | {2} | D. | {1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x≤2} | B. | {-1,0,1,2} | C. | {-2,-1,0,1,2} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 它们的焦距相等 | B. | 它们的焦点在同一个圆上 | ||
| C. | 它们的渐近线方程相同 | D. | 它们的离心率相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 6 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com