
已知抛物线C: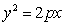 (
(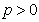 )的焦点为F(1,0),点O为坐标原点,A,B是曲线C上异于O的两点.
)的焦点为F(1,0),点O为坐标原点,A,B是曲线C上异于O的两点.
(Ⅰ)求曲线C的方程;
(Ⅱ)若直线OA,OB的斜率之积为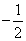 ,求证:直线AB过定点.
,求证:直线AB过定点.
解:(Ⅰ)∵焦点为F(1,0),∴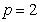 ,∴抛物线方程为
,∴抛物线方程为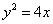 .
.
(Ⅱ)方法一:∵直线OA、OB的斜率之积为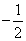
∴设直线OA的方程为 ;直线OB的方程为
;直线OB的方程为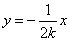 .
.
联立 得
得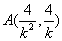 ,同理
,同理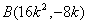
由抛物线关于x轴对称可知定点在x轴上,那么当A,B横坐标相同时的横坐标即为定点的横坐标.
令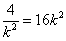 ,解得
,解得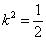 ,则
,则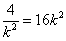 =8,点M(8,0)为直线AB过的定点.
=8,点M(8,0)为直线AB过的定点.
下面证明直线AB过M点
∵ 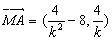 ,
,
由 可知向量
可知向量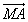 与
与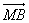 共线.
共线.
∴直线AB过定点M.
方法二:设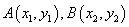 .
.
(1)若直线AB斜率存在,设其方程为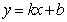
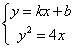 即
即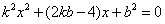 .
.
∴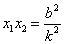 ,
,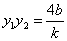 .
.
∵直线OA、OB的斜率之积为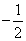 ,即
,即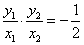 ,
,
∴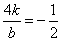 ,即
,即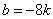 ,带入直线方程,得直线AB方程为
,带入直线方程,得直线AB方程为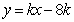 .
.
∴即直线AB过定点(8,0).
(2)若直线AB斜率不存在,则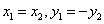 ,
,
由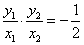 可得
可得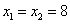 ,
,
∴直线AB方程为 ,过定点(8,0).
,过定点(8,0).
综上,直线AB过定点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年江苏省宿迁市高三下学期期初开学联考理科数学试卷(解析版) 题型:填空题
如图,点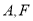 分别是椭圆
分别是椭圆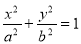
 的上顶点和右焦点,直线
的上顶点和右焦点,直线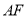 与椭圆交于另一点
与椭圆交于另一点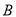 ,过中心
,过中心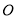 作直线
作直线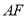 的平行线交椭圆于
的平行线交椭圆于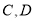 两点,若
两点,若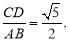 则椭圆的离心率为 .
则椭圆的离心率为 .

查看答案和解析>>
科目:高中数学 来源: 题型:
命题甲:f(x)是 R上的单调递增函数;命题乙:∃x1<x2,f(x1)<f(x2).则甲是乙的
(A)充分不必要条件 (B)必要不充分条件
(C)充分且必要条件 (D)既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
从某项综合能力测试中抽取50人的成绩,统计如下表,则这50人成绩的平
均数为__________,方差为__________.
| 分数 | 5 | 4 | 3 | 2 | 1 |
| 人数 | 10 | 5 | 15 | 15 | 5 |
(注:s2=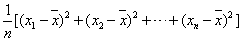 ,
,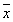 为数据
为数据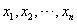 的平均数)
的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,在正方体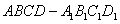 中,点
中,点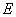 是棱
是棱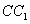 上的一个动点,平面
上的一个动点,平面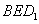 交棱
交棱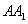 于点
于点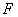 .则下列命题中假命题是 ( )
.则下列命题中假命题是 ( )
 (A)存在点
(A)存在点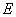 ,使得
,使得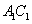 //平面
//平面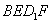
(B)存在点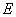 ,使得
,使得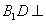 平面
平面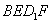
(C)对于任意的点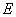 ,平面
,平面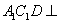 平面
平面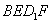
(D)对于任意的点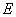 ,四棱锥
,四棱锥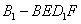 的体积均不变
的体积均不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com