考点:直线与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(1)根据勾股定理的逆定理,可得AB⊥AC,又因为四边形A1ABB1是正方形,所以AB⊥AA1,从而得到AB⊥平面AA1C,再证AB∥A1B1,可得A1B1⊥平面AA1C;
(2)取BC中点D,连接AD,B1D,C1D.证明四边形B1C1DB是平行四边形,可得C1D∥B1B,进而可证AD∥平面A1C1C;同理,B1D∥平面A1C1C,利用面面平行的判定,可得平面ADB 1∥平面A1C1C,从而可得AB1∥平面A1C1C
解答:

证明:(1)因为AB=AC,
BC=AB所以AB
2+AC
2=BC
2,所以AB⊥AC.
又因为四边形A
1ABB
1是正方形,所以AB⊥AA
1.
又因为AA
1∩AC=A,所以AB⊥平面AA
1C.
因为四边形A
1ABB
1是正方形,所以AB∥A
1B
1,
所以A
1B
1⊥平面AA
1C
(2)取BC的中点D,连接AD,B
1D,C
1D
因为B
1C
1∥BC且
B1C1=BC所以B
1C
1DB是平行四边形,故C
1D
1∥B
1B,且C
1D
1=B
1B
又A
1A∥B
1B且A
1A=B
1B,所以A
1A∥C
1D,且A
1A=C
1D
所以A
1ADC
1是平行四边形
所以A
1C
1∥AD,所以AD∥平面A
1C
1C
同理B
1D∥平面A
1C
1C
又因为B
1D∩AD=D,所以平面ADB
1∥平面A
1C
1C
所以AB
1∥平面A
1C
1C
点评:本题考查线面平行、线面垂直,掌握线面平行、线面垂直的判定方法是关键.

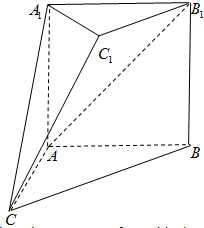 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC= 证明:(1)因为AB=AC,BC=
证明:(1)因为AB=AC,BC=

 如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2