考点:函数的图象
专题:函数的性质及应用
分析:显然该函数是奇函数,由图象分析可知,正方形的中心应过原点,且两对角线也过原点且分别关于原点对称、相互垂直,据此可设两对角线所在直线方程为y=kx,及y=-
x,分别与函数y=-4x
3+3x联立,求出交点坐标,利用两对角线长度相等列出关于k的方程,判断根的个数即可.
解答:
解:∵正方形的四个顶点均在y=-4x
3+3x的图象上,且该函数是奇函数,
所以正方形的中心过原点,由此设两对角线所在直线方程为:y=kx,及y=
-x,
由
得4x
2=3-k,
∴x=
或-,且k<3①,
将两根代入y=kx,得正方形一条对角线两交点为A(
,
),C(
-,
-);
同理,将y=
-x代入y=-4x
3+3x得4x
2=
3+,k>0或k
<-②,
x=
或
-,分别代入y=
-x得B(
,
-),D(
-,
),
根据|OA|=|OB|得
+=
(3+)+
(3+),
整理得(
)
•=0,
∴k
2-k-1=0,或k
2-2k-1=0
易知,这两个方程的两根之积都为-1,且根都满足条件①②,
∴符合题意的正方形有2个.
故答案为:2.
点评:本题充分利用该函数的奇偶性以及正方形的对称性,分析出正方形的中心是原点,且对角线互相垂直相等,通过列方程求k是解本题的关键,而由已知得到k应满足的范围,则是问题的易错点.



 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案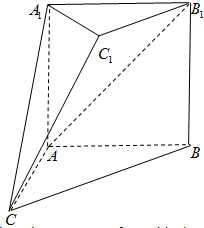 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=