
(1)求k的取值范围;
(2)如果|AB|=6![]() ,且曲线E上存在点C,使
,且曲线E上存在点C,使![]() +
+![]() =m
=m![]() ,求m的值和△ABC的面积S.
,求m的值和△ABC的面积S.
解:(1)由双曲线的定义可知,曲线E是以F1(-![]() ,0)、F2(
,0)、F2(![]() ,0)为焦点的双曲线的左支,且c=2,a=1,易知b=1.
,0)为焦点的双曲线的左支,且c=2,a=1,易知b=1.
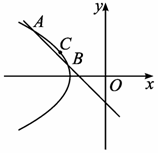
故曲线E的方程为x2-y2=1(x<0).
设A(x1,y1),B(x2,y2),由题意建立方程组
消去y,得(1-k2)x2+2kx-2=0.
又已知直线与双曲线左支交于A、B两点,有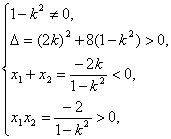
解得-![]() <k<-1.
<k<-1.
(2) 因为|AB|=![]() |x1-x2|
|x1-x2|
 2
2
依题意得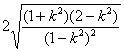 =63.
=63.
整理后得28k4-55k2+25=0.
∴k2=![]() 或k2=
或k2=![]() .
.
但-![]() <k<-1,∴k=-
<k<-1,∴k=-![]() .
.
故直线AB的方程为![]() x+y+1=0.
x+y+1=0.
设C(xc,yc),由已知![]() +
+![]() =m
=m![]() ,得(x1,y1)+(x2,y2)=(mxC,myC),
,得(x1,y1)+(x2,y2)=(mxC,myC),
∴(xC,yC)=![]() (m≠0).
(m≠0).
又x1+x2=![]() =-4
=-4![]() ,y1+y2=k(x1+x2)-2=
,y1+y2=k(x1+x2)-2=![]() -2=
-2=![]() =8,
=8,
∴点C(![]() ).
).
将点C的坐标代入曲线E的方程,得![]() =1.
=1.
得m=±4.但当m=-4时,所得的点在双曲线的右支上,不合题意.
∴m=4,C点坐标为(-![]() ,2).
,2).
C到AB的距离为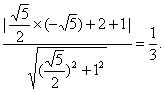
∴△ABC的面积S=![]()


科目:高中数学 来源: 题型:
| 2 |
| 2 |
| MA |
| MB |
| 1 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 2 |
| PF2 |
| PF1 |
| AB |
2
| ||
| 3 |
| OA |
| OB |
| OD |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 2 |
| PF2 |
| PF1 |
| 3 |
| OA |
| OB |
| OC |
| 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com