
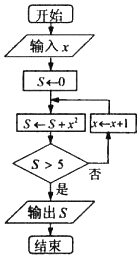
 据记载,在公元前3世纪,阿基米德已经得出了前n个自然数平方和的一般公式.如图是一个求前n个自然数平方和的算法流程图,若输入x的值为1,则输出的S的值为14.
据记载,在公元前3世纪,阿基米德已经得出了前n个自然数平方和的一般公式.如图是一个求前n个自然数平方和的算法流程图,若输入x的值为1,则输出的S的值为14. 科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
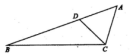 如图,在△ABC中,D为线段AB上的点,且AB=3AD,AC=AD,CB=3CD,则$\frac{sin2B}{sinA}$=$\frac{7}{9}$.
如图,在△ABC中,D为线段AB上的点,且AB=3AD,AC=AD,CB=3CD,则$\frac{sin2B}{sinA}$=$\frac{7}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -6 | C. | 15 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com