
分析 (1)λ=3,μ=8时,an+1=$\frac{3{a}_{n}^{2}+8{a}_{n}+4}{{a}_{n}+2}$=3an+2,化为:an+1+1=3(an+1),即可证明.
(2)①设an=a1+(n-1)d=dn-d+1.由an+1=$\frac{{λ{a_n}^2+μ{a_n}+4}}{{{a_n}+2}}$,可得:an+1(an+2)=$λ{a}_{n}^{2}+μ{a}_{n}$+4,
(dn-d+3)(dn+1)=λ(dn-d+1)2+μ(dn-d+1)+4,令n=1,2,3,解出即可得出..
②由①可得:Sn=$\frac{n(1+2n-1)}{2}$=n2.设存在首项为S1的四项子数列,使得该子数列中点所有项之和恰好为2017.
则这四项为:三个奇数一个偶数,或者三个偶数一个奇数.
1°三个奇数一个偶数:设S1,S2x+1,S2y+1,S2z是满足条件的四项,则1+(2x+1)2+(2y+1)2+(2z)2=2017,化为2(x2+x+y2+y+z2)=1007,矛盾,舍去.
2°三个偶数一个奇数,设S1,S2x,S2y,S2z是满足条件的四项,则1+(2x)2+(2y)2+(2z)2=2017,化为x2+y2+z2=504.由504为偶数,x,y,z中一个偶数两个奇数或者三个偶数.
(i)若x,y,z中一个偶数两个奇数,不妨设x=2x1,y=2y1+1,z=2z1+1,则2$({x}_{1}^{2}+{y}_{1}^{2}+{y}_{1}+{z}_{1}^{2}+{z}_{1})$=251,矛盾.
(ii)若x,y,z均为偶数,不妨设x=2x1,y=2y1,z=2z1,则${x}_{1}^{2}$+${y}_{1}^{2}$+${z}_{1}^{2}$=126,则x1,y1,z1中有两个奇数一个偶数.不妨设x1=2x2,y1=2y2+1,z1=2z2+1,则${x}_{2}^{2}+{y}_{2}^{2}+{y}_{2}+{z}_{2}^{2}+{z}_{2}$=31.依此类推分类讨论即可得出.
解答 (1)证明:λ=3,μ=8时,an+1=$\frac{3{a}_{n}^{2}+8{a}_{n}+4}{{a}_{n}+2}$=3an+2,化为:an+1+1=3(an+1),
∴:{an+1}为等比数列,首项为2,公比为3.
∴an+1=2×3n-1,可得:an=2×3n-1-1.
(2)解:①设an=a1+(n-1)d=dn-d+1.由an+1=$\frac{{λ{a_n}^2+μ{a_n}+4}}{{{a_n}+2}}$,可得:an+1(an+2)=$λ{a}_{n}^{2}+μ{a}_{n}$+4,
∴(dn-d+3)(dn+1)=λ(dn-d+1)2+μ(dn-d+1)+4,
令n=1,2,3,解得:λ=1,μ=4,d=2.
经过检验满足题意,可得:λ=1,μ=4,an=2n-1.
②由①可得:Sn=$\frac{n(1+2n-1)}{2}$=n2.设存在首项为S1的四项子数列,使得该子数列中点所有项之和恰好为2017.
则这四项为:三个奇数一个偶数,或者三个偶数一个奇数.1°三个奇数一个偶数:设S1,S2x+1,S2y+1,S2z是满足条件的四项,则1+(2x+1)2+(2y+1)2+(2z)2=2017,化为2(x2+x+y2+y+z2)=1007,矛盾,舍去.
2°三个偶数一个奇数,设S1,S2x,S2y,S2z是满足条件的四项,则1+(2x)2+(2y)2+(2z)2=2017,化为x2+y2+z2=504.由504为偶数,x,y,z中一个偶数两个奇数或者三个偶数.
(i)若x,y,z中一个偶数两个奇数,不妨设x=2x1,y=2y1+1,z=2z1+1,则2$({x}_{1}^{2}+{y}_{1}^{2}+{y}_{1}+{z}_{1}^{2}+{z}_{1})$=251,矛盾.
(ii)若x,y,z均为偶数,不妨设x=2x1,y=2y1,z=2z1,则${x}_{1}^{2}$+${y}_{1}^{2}$+${z}_{1}^{2}$=126,则x1,y1,z1中有两个奇数一个偶数.不妨设x1=2x2,y1=2y2+1,z1=2z2+1,则${x}_{2}^{2}+{y}_{2}^{2}+{y}_{2}+{z}_{2}^{2}+{z}_{2}$=31.
∵y2(y2+1),z2(z2+1)均为偶数,∴x2为奇数.不妨设0≤y2≤z2.
当x2=1时,则${y}_{2}^{2}$+y2+${z}_{2}^{2}$+z2=30,${y}_{2}^{2}$+y2≤14,检验可得:y2=0,z2=5,x2=1.
当x2=3时,则${y}_{2}^{2}$+y2+${z}_{2}^{2}$+z2=22,${y}_{2}^{2}$+y2≤10,检验可得:y2=1,z2=4,x2=3.
当x2=5时,则${y}_{2}^{2}$+y2+${z}_{2}^{2}$+z2=6,${y}_{2}^{2}$+y2≤2,检验可得:y2=0,z2=2,x2=5.
即{S1,S4,S8,S44},{S1,S12,S24,S36},{S1,S4,S20,S40}为全部满足条件的四元子列.
点评 本题考查了数列递推关系、数列通项公式、分类讨论方法、数奇偶性,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | $-\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
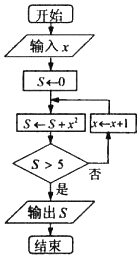 据记载,在公元前3世纪,阿基米德已经得出了前n个自然数平方和的一般公式.如图是一个求前n个自然数平方和的算法流程图,若输入x的值为1,则输出的S的值为14.
据记载,在公元前3世纪,阿基米德已经得出了前n个自然数平方和的一般公式.如图是一个求前n个自然数平方和的算法流程图,若输入x的值为1,则输出的S的值为14.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,e) | B. | (-∞,e] | C. | $(-∞,\frac{1}{e})$ | D. | $(-∞,\frac{1}{e}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com