
| A. | (-∞,e) | B. | (-∞,e] | C. | $(-∞,\frac{1}{e})$ | D. | $(-∞,\frac{1}{e}]$ |
分析 由题意可知f(x)=-g(x)有解,即y=lnx与y=ax有交点,根据导数的几何意义,求出切点,结合图象,可知a的范围.
解答 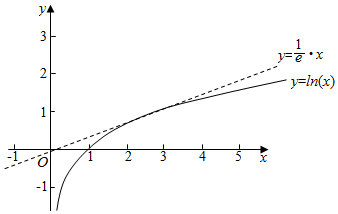 解:函数f(x)=lnx-x3与g(x)=x3-ax的图象上存在关于x轴的对称点,
解:函数f(x)=lnx-x3与g(x)=x3-ax的图象上存在关于x轴的对称点,
∴f(x)=-g(x)有解,
∴lnx-x3=-x3+ax,
∴lnx=ax,在(0,+∞)有解,
分别设y=lnx,y=ax,
若y=ax为y=lnx的切线,
∴y′=$\frac{1}{x}$,
设切点为(x0,y0),
∴a=$\frac{1}{{x}_{0}}$,ax0=lnx0,
∴x0=e,
∴a=$\frac{1}{e}$,
结合图象可知,a≤$\frac{1}{e}$
故选:D.
点评 本题导数的几何意义,以及函数与方程的综合应用问题,关键是转化为y=lnx与y=ax有交点,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
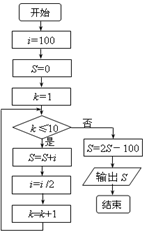 一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( )
一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( )| A. | 小球第10次着地时向下的运动共经过的路程 | |
| B. | 小球第11次着地时向下的运动共经过的路程 | |
| C. | 小球第10次着地时一共经过的路程 | |
| D. | 小球第11次着地时一共经过的路程 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
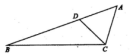 如图,在△ABC中,D为线段AB上的点,且AB=3AD,AC=AD,CB=3CD,则$\frac{sin2B}{sinA}$=$\frac{7}{9}$.
如图,在△ABC中,D为线段AB上的点,且AB=3AD,AC=AD,CB=3CD,则$\frac{sin2B}{sinA}$=$\frac{7}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{10}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{4\sqrt{5}}}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com