
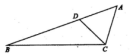
 如图,在△ABC中,D为线段AB上的点,且AB=3AD,AC=AD,CB=3CD,则$\frac{sin2B}{sinA}$=$\frac{7}{9}$.
如图,在△ABC中,D为线段AB上的点,且AB=3AD,AC=AD,CB=3CD,则$\frac{sin2B}{sinA}$=$\frac{7}{9}$. 分析 设AC=x,CD=y,则AB=3x,BC=3y;
利用余弦定理求出x2、y2的关系,再用二倍角化简$\frac{sin2B}{sinA}$,
利用正弦、余弦定理即可求出结果.
解答 解:设AC=x,CD=y,则AB=3x,BC=3y;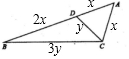
∴cosA=$\frac{{x}^{2}{+x}^{2}{-y}^{2}}{2•x•x}$=$\frac{{9x}^{2}{+x}^{2}-{9y}^{2}}{2•3x•x}$,
化简得x2=$\frac{3}{2}$y2;
∴$\frac{sin2B}{sinA}$=$\frac{2sinBcosB}{sinA}$
=2•$\frac{x}{3y}$•$\frac{{9x}^{2}+{9y}^{2}{-x}^{2}}{2•3x•3y}$
=$\frac{{8x}^{2}+{9y}^{2}}{2{7y}^{2}}$
=$\frac{8}{27}$•$\frac{3}{2}$+$\frac{1}{3}$
=$\frac{7}{9}$.
故答案为:$\frac{7}{9}$.
点评 本题考查了正弦、余弦定理的灵活应用问题,是综合题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
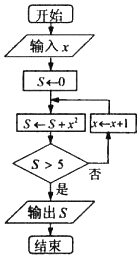 据记载,在公元前3世纪,阿基米德已经得出了前n个自然数平方和的一般公式.如图是一个求前n个自然数平方和的算法流程图,若输入x的值为1,则输出的S的值为14.
据记载,在公元前3世纪,阿基米德已经得出了前n个自然数平方和的一般公式.如图是一个求前n个自然数平方和的算法流程图,若输入x的值为1,则输出的S的值为14.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,e) | B. | (-∞,e] | C. | $(-∞,\frac{1}{e})$ | D. | $(-∞,\frac{1}{e}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com