

 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题p∨q为假命题 | B. | 命题p∧q为真命题 | ||
| C. | 命题p∧(¬q)为真命题 | D. | 命题p∨(¬q)为假命题 | ||
| E. | 命题p∨q为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±x | B. | $y=±\sqrt{2}x$ | C. | $y=±\sqrt{3}x$ | D. | y=±2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
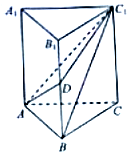 如图,在直三棱柱ABC-A1B1C1中,AB=1,BC=2,BB1=3,∠ABC=90°,点D为侧棱BB1上的动点,当AD+DC1最小时,三棱锥D-ABC1的体积为$\frac{1}{3}$.
如图,在直三棱柱ABC-A1B1C1中,AB=1,BC=2,BB1=3,∠ABC=90°,点D为侧棱BB1上的动点,当AD+DC1最小时,三棱锥D-ABC1的体积为$\frac{1}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
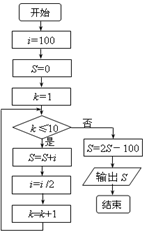 一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( )
一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( )| A. | 小球第10次着地时向下的运动共经过的路程 | |
| B. | 小球第11次着地时向下的运动共经过的路程 | |
| C. | 小球第10次着地时一共经过的路程 | |
| D. | 小球第11次着地时一共经过的路程 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
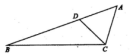 如图,在△ABC中,D为线段AB上的点,且AB=3AD,AC=AD,CB=3CD,则$\frac{sin2B}{sinA}$=$\frac{7}{9}$.
如图,在△ABC中,D为线段AB上的点,且AB=3AD,AC=AD,CB=3CD,则$\frac{sin2B}{sinA}$=$\frac{7}{9}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com