练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
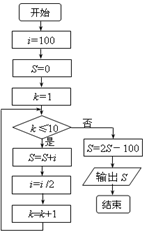
    20．一个小球从100米高处自由落下，每次着地后又跳回到原高度的一半再落下．执行下面的程序框图，则输出的S表示的是（　　）
    A．小球第10次着地时向下的运动共经过的路程
    B．小球第11次着地时向下的运动共经过的路程
    C．小球第10次着地时一共经过的路程
    D．小球第11次着地时一共经过的路程

    分析 分析程序框图的运行过程，知程序运行后输出的S
    是小球第10次着地时一共经过的路程．

    解答 解：执行该程序框图知，该程序运行后输出的是
    S=2×（100+50+25+…+$\frac{100}{{2}^{9}}$）-100，
    它表示小球第10次着地时一共经过的路程．
    故选：C．

    点评 本题考查了利用程序框图进行累加计算的问题，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    10．设常数λ＞0，a＞0，f（x）=$\frac{{x}^{2}}{λ+x}$-alnx
    （1）若f（x）在x=λ处取得极小值为0，求λ和a的值；
    （2）对于任意给定的正实数λ、a，证明：存在实数x0，当x＞x0时，f（x）＞0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．执行如图所示的伪代码，若输出的y值为1，则输入x的值为-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知等差数列{an}前5项和为50，a7=22，数列{bn}的前n项和为Sn，b1=1，bn+1=3Sn+1．
    （Ⅰ）求数列{an}，{bn}的通项公式；
    （Ⅱ）若数列{cn}满足$\frac{c_1}{b_1}+\frac{c_2}{b_2}+…+\frac{c_n}{b_n}={a_{n+1}}$，n∈N*，求c1+c2+…+c2017的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．复数$z=\frac{-1+i}{2-i}$的虚部为（　　）
    A．$-\frac{3}{5}$B．$\frac{3}{5}$C．$\frac{1}{5}$D．$-\frac{1}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．漳州水仙鳞茎硕大，箭多花繁，色美香郁，素雅娟丽，有“天下水仙数漳州”之美誉．现某水仙花雕刻师受雇每天雕刻250粒水仙花，雕刻师每雕刻一粒可赚1.2元，如果雕刻师当天超额完成任务，则超出的部分每粒赚1.7元；如果当天未能按量完成任务，则按实际完成的雕刻量领取当天工资．
    （I）求雕刻师当天收入（单位：元）关于雕刻量n（单位：粒，n∈N）的函数解析式f（n）；
    （Ⅱ）该雕刻师记录了过去10天每天的雕刻量n（单位：粒），整理得如表：
    雕刻量n210230250270300
    频数12331
    以10天记录的各雕刻量的频率作为各雕刻量发生的概率．
    （ⅰ）求该雕刻师这10天的平均收入；
    （ⅱ）求该雕刻师当天收入不低于300元的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2．
    （1）求A1到平面AB1D距离；
    （2）求D到平面A1BD1距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．在△ABC中，角A，B，C的对边分别为a，b，c，且a，b，c成等比数列，若tan B=$\frac{3}{4}$，$\frac{cosA}{sinA}$+$\frac{cosC}{sinC}$的值为（　　）
    A．$\frac{5}{4}$B．$\frac{5}{3}$C．$\frac{4}{5}$D．$\frac{3}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知函数f（x）=lnx-x3与g（x）=x3-ax的图象上存在关于x轴的对称点，则实数a的取值范围为（　　）
    A．（-∞，e）B．（-∞，e]C．$（-∞，\frac{1}{e}）$D．$（-∞，\frac{1}{e}]$

    查看答案和解析>>

    同步练习册答案