
分析 (1)解方程组$\left\{\begin{array}{l}{f(λ)=0}\\{f′(λ)=0}\end{array}\right.$即可得出λ和a的值;
(2)f(x)>x-λ-alnx,令h(x)=x-λ-alnx=x-a$\sqrt{x}$-λ+a($\sqrt{x}$-lnx),证明$\sqrt{x}$-lnx>0,则f(x)>0转化为证明h(x)>0,转化为x-a$\sqrt{x}$-λ≥0,解出x即可得出符合条件的x0.
解答 解:(1)f′(x)=$\frac{2x(λ+x)-{x}^{2}}{(x+λ)^{2}}$-$\frac{a}{x}$=$\frac{{x}^{3}+2λ{x}^{2}-a(x+λ)^{2}}{x(x+λ)^{2}}$,
∵f(x)在x=λ处取得极小值0,∴$\left\{\begin{array}{l}{f′(λ)=0}\\{f(λ)=0}\end{array}\right.$,
即$\left\{\begin{array}{l}{3{λ}^{3}-4a{λ}^{2}=0}\\{\frac{λ}{2}-alnλ=0}\end{array}\right.$,解得λ=e${\;}^{\frac{2}{3}}$,a=$\frac{3}{4}{e}^{\frac{2}{3}}$.
(Ⅱ)f(x)=$\frac{{x}^{2}}{λ+x}$-alnx=x-λ+$\frac{{λ}^{2}}{x+λ}$-alnx>x-λ-alnx,
令h(x)=x-λ-alnx,故只需证明:存在实数x0,当x>x0时,h(x)>0,
h(x)=x-λ-alnx=x-a$\sqrt{x}$-λ+a($\sqrt{x}$-lnx),
设y=$\sqrt{x}$-lnx,则y′=$\frac{1}{2\sqrt{x}}-\frac{1}{x}$=$\frac{\sqrt{x}-2}{2x}$.
∴当0<x<4时,y′<0,当x>4时,y′>0,
∴当x=4时,y=$\sqrt{x}$-lnx取得最小值2-2ln2>0,∴y=$\sqrt{x}$-lnx>0.
令x-a$\sqrt{x}$-λ≥0,即($\sqrt{x}$)2-a$\sqrt{x}$-λ≥0,解得:$\sqrt{x}$≥$\frac{a+\sqrt{{a}^{2}+4λ}}{2}$,即x≥($\frac{a+\sqrt{{a}^{2}+4λ}}{2}$)2,
取x0=($\frac{a+\sqrt{{a}^{2}+4λ}}{2}$)2,则当x>x0时,恒有h(x)>0.
∴当x>x0时,恒有f(x)>0恒成立.
点评 本题考查了导数与函数单调性、函数极值的关系,函数恒等式的证明,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p∨q为假命题 | B. | 命题p∧q为真命题 | ||
| C. | 命题p∧(¬q)为真命题 | D. | 命题p∨(¬q)为假命题 | ||
| E. | 命题p∨q为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
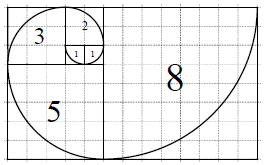 斐波那契数列{an}满足:${a_1}=1,{a_2}=1,{a_n}={a_{n-1}}+{a_{n-2}}({n≥3,n∈{N^*}})$.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前n项所占的格子的面积之和为Sn,每段螺旋线与其所在的正方形所围成的扇形面积为cn,则下列结论错误的是( )
斐波那契数列{an}满足:${a_1}=1,{a_2}=1,{a_n}={a_{n-1}}+{a_{n-2}}({n≥3,n∈{N^*}})$.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前n项所占的格子的面积之和为Sn,每段螺旋线与其所在的正方形所围成的扇形面积为cn,则下列结论错误的是( )| A. | ${S_{n+1}}=a_{n+1}^2+{a_{n+1}}•{a_n}$ | B. | a1+a2+a3+…+an=an+2-1 | ||
| C. | a1+a3+a5+…+a2n-1=a2n-1 | D. | 4(cn-cn-1)=πan-2•an+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±x | B. | $y=±\sqrt{2}x$ | C. | $y=±\sqrt{3}x$ | D. | y=±2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
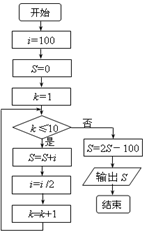 一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( )
一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( )| A. | 小球第10次着地时向下的运动共经过的路程 | |
| B. | 小球第11次着地时向下的运动共经过的路程 | |
| C. | 小球第10次着地时一共经过的路程 | |
| D. | 小球第11次着地时一共经过的路程 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com