
| 雕刻量n | 210 | 230 | 250 | 270 | 300 |
| 频数 | 1 | 2 | 3 | 3 | 1 |
分析 (Ⅰ)当n≥250时,f(n)=250×1.2+1.7×(n-250),当n<250时,f(n)=1.2n,由此能求出雕刻师当天收入(单位:元)关于雕刻量n(单位:粒,n∈N)的函数解析式.
(Ⅱ)(i)由题意得f(210)=252,f(230)=276,f(250)=300,f(270)=334,f(300)=385,X的可能取值为252,276,300,334,385,分别求出相应的概率,由此能求出该雕刻师这10天的平均收入.
(ii)由X的分布列知该雕刻师当天收入不低于300元的概率:P=P(X=300)+P(X=334)+P(X=385),由此能求出结果.
解答 解:(Ⅰ)当n≥250时,f(n)=250×1.2+1.7×(n-250)=1.7n-125,
当n<250时,f(n)=1.2n,
∴雕刻师当天收入(单位:元)关于雕刻量n(单位:粒,n∈N)的函数解析式:
f(n)=$\left\{\begin{array}{l}{1.7n-125,n≥250}\\{1.2n,n<250}\end{array}\right.$,(n∈N).
(Ⅱ)(i)由题意得f(210)=252,f(230)=276,f(250)=300,f(270)=334,f(300)=385,
∴X的可能取值为252,276,300,334,385,
P(X=252)=0.1,P(X=276)=0.2,P(X=300)=0.3,
P(X=334)=0.3,P(X=385)=0.1,
∴X的分布列为:
| X | 252 | 276 | 300 | 334 | 385 |
| P | 0.1 | 0.2 | 0.3 | 0.3 | 0.1 |
点评 本题考查函数解析式的求法,考查离散型随机的分布列、数学期望等基础知识,考查推理论证能力、运算求解能力、空间思维能力,考查数形结合思想、化归与转化思想,是中档题.


科目:高中数学 来源: 题型:选择题
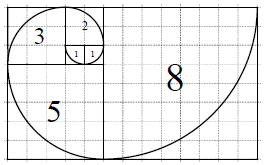 斐波那契数列{an}满足:${a_1}=1,{a_2}=1,{a_n}={a_{n-1}}+{a_{n-2}}({n≥3,n∈{N^*}})$.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前n项所占的格子的面积之和为Sn,每段螺旋线与其所在的正方形所围成的扇形面积为cn,则下列结论错误的是( )
斐波那契数列{an}满足:${a_1}=1,{a_2}=1,{a_n}={a_{n-1}}+{a_{n-2}}({n≥3,n∈{N^*}})$.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前n项所占的格子的面积之和为Sn,每段螺旋线与其所在的正方形所围成的扇形面积为cn,则下列结论错误的是( )| A. | ${S_{n+1}}=a_{n+1}^2+{a_{n+1}}•{a_n}$ | B. | a1+a2+a3+…+an=an+2-1 | ||
| C. | a1+a3+a5+…+a2n-1=a2n-1 | D. | 4(cn-cn-1)=πan-2•an+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
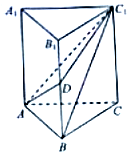 如图,在直三棱柱ABC-A1B1C1中,AB=1,BC=2,BB1=3,∠ABC=90°,点D为侧棱BB1上的动点,当AD+DC1最小时,三棱锥D-ABC1的体积为$\frac{1}{3}$.
如图,在直三棱柱ABC-A1B1C1中,AB=1,BC=2,BB1=3,∠ABC=90°,点D为侧棱BB1上的动点,当AD+DC1最小时,三棱锥D-ABC1的体积为$\frac{1}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
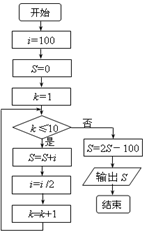 一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( )
一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( )| A. | 小球第10次着地时向下的运动共经过的路程 | |
| B. | 小球第11次着地时向下的运动共经过的路程 | |
| C. | 小球第10次着地时一共经过的路程 | |
| D. | 小球第11次着地时一共经过的路程 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
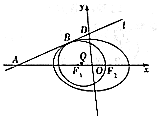 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,过点A(-4,0)的直线l与椭圆C相切于点B,与y轴交于点D(0,2),又椭圆的离心率为$\frac{1}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,过点A(-4,0)的直线l与椭圆C相切于点B,与y轴交于点D(0,2),又椭圆的离心率为$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com