
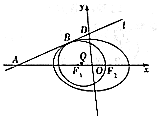
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,过点A(-4,0)的直线l与椭圆C相切于点B,与y轴交于点D(0,2),又椭圆的离心率为$\frac{1}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,过点A(-4,0)的直线l与椭圆C相切于点B,与y轴交于点D(0,2),又椭圆的离心率为$\frac{1}{2}$.分析 (1)求出直线l的方程,代入椭圆方程消元,令△=0得出a,b的关系,结合e=$\frac{1}{2}$求出a,b;
(2)求出B点坐标,得出BF2的中垂线方程和直线BQ的方程,联立方程组求出Q点坐标,计算圆的半径,得出圆Q的方程,比较圆心距与两圆半径的大小关系得出两圆的位置关系.
解答 解:(1)直线l的方程为y=$\frac{1}{2}$x+2,
联立方程组$\left\{\begin{array}{l}{y=\frac{1}{2}x+2}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,消元得($\frac{1}{4}{a}^{2}+{b}^{2}$)x2+2a2x+4a2-a2b2=0,
∵直线l与椭圆相切,∴△=4a4-4($\frac{1}{4}{a}^{2}+{b}^{2}$)(4a2-a2b2)=0,
即a2+4b2-16=0.①
∵e=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{1}{2}$,∴b2=$\frac{3}{4}{a}^{2}$,②
由①②可得a2=4,b2=3,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(2)由(1)可得4x2+8x+4=0,解得x=-1,把x=-1代入y=$\frac{1}{2}$x+2得y=$\frac{3}{2}$,
∴B(-1,$\frac{3}{2}$),又F2(1,0),∴BF2的中点坐标为(0,$\frac{3}{4}$),K${\;}_{B{F}_{2}}$=-$\frac{3}{4}$,
∴直线BQ的方程为y-$\frac{3}{2}$=-2(x+1),即y=-2x-$\frac{1}{2}$.
BF2的中垂线方程为y=$\frac{4}{3}$x+$\frac{3}{4}$.
联立方程组$\left\{\begin{array}{l}{y=-2x-\frac{1}{2}}\\{y=\frac{4}{3}x+\frac{3}{4}}\end{array}\right.$得$\left\{\begin{array}{l}{x=-\frac{3}{8}}\\{y=\frac{1}{4}}\end{array}\right.$,
∴Q的坐标为(-$\frac{3}{8}$,$\frac{1}{4}$),圆Q的半径为|QF2|=$\sqrt{(-\frac{3}{8}-1)^{2}+(\frac{1}{4})^{2}}$=$\frac{5\sqrt{5}}{8}$,
∴圆Q的方程为(x+$\frac{3}{8}$)2+(y-$\frac{1}{4}$)2=$\frac{125}{64}$.
∵|OQ|=$\frac{\sqrt{31}}{8}$,∴2-$\frac{5\sqrt{5}}{8}$<OQ<2+$\frac{5\sqrt{5}}{8}$,
∴圆Q与圆x2+y2=a2相交.
点评 本题考查了椭圆的性质,直线与圆的位置关系,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
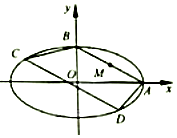 如图,在平面直角坐标系xoy中,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点和上顶点分别为点A,B,M是线段AB的中点,且$\overrightarrow{OM}•\overrightarrow{AB}=-\frac{3}{2}{b^2}$..
如图,在平面直角坐标系xoy中,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点和上顶点分别为点A,B,M是线段AB的中点,且$\overrightarrow{OM}•\overrightarrow{AB}=-\frac{3}{2}{b^2}$..查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -4 | C. | -9 | D. | -16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 雕刻量n | 210 | 230 | 250 | 270 | 300 |
| 频数 | 1 | 2 | 3 | 3 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2kπ+$\frac{π}{6}$,2kπ+$\frac{5π}{6}$),k∈Z | |
| B. | (2kπ-$\frac{π}{6}$,2kπ)∪(2kπ,2kπ+π)∪(2kπ+π,2kπ+$\frac{7}{6}$π),k∈Z | |
| C. | (2kπ-$\frac{5π}{6}$,2kπ-$\frac{π}{6}$),k∈Z | |
| D. | (2kπ-$\frac{7π}{6}$,2kπ-π)∪(2kπ-π,2kπ)∪(2kπ,2kπ+$\frac{π}{6}$),k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
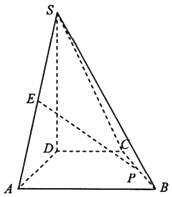 如图,在四棱锥S-ABCD中,SD⊥平面ABCD,四边形ABCD是直角梯形,∠ADC=∠DAB=90°,SD=AD=AB=2,DC=1
如图,在四棱锥S-ABCD中,SD⊥平面ABCD,四边形ABCD是直角梯形,∠ADC=∠DAB=90°,SD=AD=AB=2,DC=1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
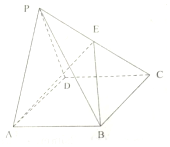 如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,△PAD为正三角形,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F,平面PCD与平面PAB交于直线l.
如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,△PAD为正三角形,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F,平面PCD与平面PAB交于直线l.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com