
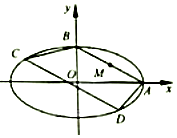
 如图,在平面直角坐标系xoy中,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点和上顶点分别为点A,B,M是线段AB的中点,且$\overrightarrow{OM}•\overrightarrow{AB}=-\frac{3}{2}{b^2}$..
如图,在平面直角坐标系xoy中,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点和上顶点分别为点A,B,M是线段AB的中点,且$\overrightarrow{OM}•\overrightarrow{AB}=-\frac{3}{2}{b^2}$..分析 (1)A(a,0),B(0,b),线段AB的中点M$(\frac{a}{2},\frac{b}{2})$.利用$\overrightarrow{OM}•\overrightarrow{AB}=-\frac{3}{2}{b^2}$与离心率的计算公式即可得出.
(2)由a=2,可得b=1,可得椭圆的标准方程为:$\frac{{x}^{2}}{4}$+y2=1,A(2,0),B(0,1).直线BC的方程为:y=k2x+1,直线AD的方程为:y=k1(x-2),分别于同一方程联立解得C,D,坐标,利用kCD=$\frac{{y}_{C}-{y}_{D}}{{x}_{C}-{x}_{D}}$=-$\frac{1}{2}$,即可得出.
解答 (1)解:A(a,0),B(0,b),线段AB的中点M$(\frac{a}{2},\frac{b}{2})$.
$\overrightarrow{AB}$=(-a,b),$\overrightarrow{OM}$=$(\frac{a}{2},\frac{b}{2})$.
∵$\overrightarrow{OM}•\overrightarrow{AB}=-\frac{3}{2}{b^2}$.
∴$-\frac{{a}^{2}}{2}$+$\frac{1}{2}{b}^{2}$=-$\frac{3}{2}$b2,化为:a=2b.
∴椭圆的离心率e=$\frac{c}{a}$=$\sqrt{1-(\frac{b}{a})^{2}}$=$\frac{\sqrt{3}}{2}$.
(2)证明:由a=2,可得b=1,
∴椭圆的标准方程为:$\frac{{x}^{2}}{4}$+y2=1,A(2,0),B(0,1).
直线BC的方程为:y=k2x+1,联立$\left\{\begin{array}{l}{y={k}_{2}x+1}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,化为:(1+$4{k}_{2}^{2}$)x2+8k2x=0,
解得xC=$\frac{-8{k}_{2}}{1+4{k}_{2}^{2}}$,∴yC=$\frac{1-4{k}_{2}^{2}}{1+4{k}_{2}^{2}}$.即C($\frac{-8{k}_{2}}{1+4{k}_{2}^{2}}$,$\frac{1-4{k}_{2}^{2}}{1+4{k}_{2}^{2}}$).
直线AD的方程为:y=k1(x-2),联立$\left\{\begin{array}{l}{y={k}_{1}(x-2)}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,化为:$(1+4{k}_{1}^{2})$x2-16${k}_{1}^{2}$x+$16{k}_{1}^{2}$-4=0,
∴2xD=$\frac{16{k}_{1}^{2}-4}{1+4{k}_{1}^{2}}$,解得xD=$\frac{8{k}_{1}^{2}-2}{1+4{k}_{1}^{2}}$,yD=$\frac{-4{k}_{1}}{1+4{k}_{1}^{2}}$,可得D($\frac{8{k}_{1}^{2}-2}{1+4{k}_{1}^{2}}$,$\frac{-4{k}_{1}}{1+4{k}_{1}^{2}}$)
∴kCD=$\frac{{y}_{C}-{y}_{D}}{{x}_{C}-{x}_{D}}$=-$\frac{1}{2}$,
化为:1-16${k}_{1}^{2}{k}_{2}^{2}$+2k1-2k2+8${k}_{1}{k}_{2}^{2}$-8${k}_{2}{k}_{1}^{2}$=0.
∴$({k}_{1}{k}_{2}-\frac{1}{4})$(4k1k2+4k1-4k2+1)=0,
∴k1k2=$\frac{1}{4}$.
点评 本题考查了椭圆的标准方程与性质、直线与椭圆相交问题、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于难题.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
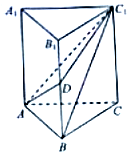 如图,在直三棱柱ABC-A1B1C1中,AB=1,BC=2,BB1=3,∠ABC=90°,点D为侧棱BB1上的动点,当AD+DC1最小时,三棱锥D-ABC1的体积为$\frac{1}{3}$.
如图,在直三棱柱ABC-A1B1C1中,AB=1,BC=2,BB1=3,∠ABC=90°,点D为侧棱BB1上的动点,当AD+DC1最小时,三棱锥D-ABC1的体积为$\frac{1}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
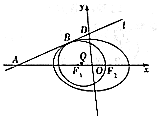 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,过点A(-4,0)的直线l与椭圆C相切于点B,与y轴交于点D(0,2),又椭圆的离心率为$\frac{1}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,过点A(-4,0)的直线l与椭圆C相切于点B,与y轴交于点D(0,2),又椭圆的离心率为$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 数据 | [12,5,15.5) | [15.5,18.5) | [18.5,21.5) | [21,5,24.5) |
| 频数 | 2 | 1 | 3 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com