
分析 根据$\overrightarrow{b}$=(1,$\sqrt{3}$)求出|$\overrightarrow{b}$|,再根据平面向量数量积与投影的定义,计算$\overrightarrow{a}$+$\overrightarrow{b}$在$\overrightarrow{b}$方向上的投影即可.
解答 解:∵$\overrightarrow{a}$•$\overrightarrow{b}$=2,且$\overrightarrow{b}$=(1,$\sqrt{3}$),
∴|$\overrightarrow{b}$|=$\sqrt{{1}^{2}{+(\sqrt{3})}^{2}}$=2,
∴($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{b}$=$\overrightarrow{a}$$•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=2+22=6,
∴$\overrightarrow{a}$+$\overrightarrow{b}$在$\overrightarrow{b}$方向上的投影为:
|$\overrightarrow{a}$+$\overrightarrow{b}$|cos<$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{b}$>=|$\overrightarrow{a}$+$\overrightarrow{b}$|×$\frac{(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{b}}{|\overrightarrow{a}+\overrightarrow{b}|×|\overrightarrow{b}|}$=$\frac{6}{2}$=3.
故答案为:3.
点评 本题考查了平面向量的数量积运算以及向量投影的应用问题,是基础题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
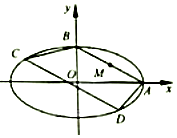 如图,在平面直角坐标系xoy中,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点和上顶点分别为点A,B,M是线段AB的中点,且$\overrightarrow{OM}•\overrightarrow{AB}=-\frac{3}{2}{b^2}$..
如图,在平面直角坐标系xoy中,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点和上顶点分别为点A,B,M是线段AB的中点,且$\overrightarrow{OM}•\overrightarrow{AB}=-\frac{3}{2}{b^2}$..查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -4 | C. | -9 | D. | -16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com