
分析 根据题意,先由双曲线的方程分析可得m的取值范围,进而又由该双曲线的焦距为6,则有c=3,即$\sqrt{2{m}^{2}+3m}$=3,解可得m的值,结合m的范围可得m的值,用集合表示即可得答案.
解答 解:根据题意,双曲线的方程为:$\frac{x^2}{{2{m^2}}}-\frac{y^2}{3m}=1$,则有$\left\{\begin{array}{l}{2{m}^{2}>0}\\{3m>0}\end{array}\right.$,解可得m>0,
则有c=$\sqrt{2{m}^{2}+3m}$,
又由该双曲线的焦距为6,则有c=3,
即$\sqrt{2{m}^{2}+3m}$=3,
解可得:m=-3或$\frac{3}{2}$,
又由m>0,
则m=$\frac{3}{2}$;
即所有满足条件的实数m构成的集合是{$\frac{3}{2}$};
故答案为:{$\frac{3}{2}$}.
点评 本题考查双曲线的几何性质,注意焦距是2c.


科目:高中数学 来源: 题型:解答题
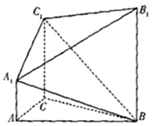 如图,在几何体A1B1C1-ABC中,∠ACB=90°,AC=BC=2,AA1⊥平面ABC,AA1∥BB1∥CC1,BB1:CC1:AA1=3:2:1,且AA1=1.
如图,在几何体A1B1C1-ABC中,∠ACB=90°,AC=BC=2,AA1⊥平面ABC,AA1∥BB1∥CC1,BB1:CC1:AA1=3:2:1,且AA1=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
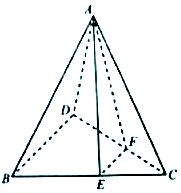 如图,在三棱锥A-BCD中,E,F分别为BC,CD上的点,且BD∥平面AEF.
如图,在三棱锥A-BCD中,E,F分别为BC,CD上的点,且BD∥平面AEF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$钱 | B. | $\frac{5}{6}$钱 | C. | 1钱 | D. | $\frac{7}{6}$钱 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com