
分析 由已知利用同角三角函数基本关系式可求cosα,tanα的值,进而利用两角和的正切函数公式即可计算得解.
解答 解:∵α是第二象限角,且sinα=$\frac{3}{{\sqrt{10}}},tan({α+β})=-2$,
∴cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{\sqrt{10}}{10}$,tanα=-3,
$\frac{tanα+tanβ}{1-tanαtanβ}$=$\frac{tanβ-3}{1+3tanβ}$=-2,
∴tanβ=$\frac{1}{7}$.
故答案为:$\frac{1}{7}$.
点评 本题主要考查了同角三角函数基本关系式,两角和的正切函数公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 3$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$钱 | B. | $\frac{5}{6}$钱 | C. | 1钱 | D. | $\frac{7}{6}$钱 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 数据 | [12,5,15.5) | [15.5,18.5) | [18.5,21.5) | [21,5,24.5) |
| 频数 | 2 | 1 | 3 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
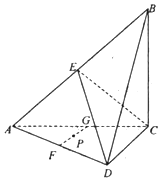 如图,在四面体ABCD中,平面ABC⊥平面ACD,E,F,G分别为AB,AD,AC的中点,AC=BC,∠ACD=90°.
如图,在四面体ABCD中,平面ABC⊥平面ACD,E,F,G分别为AB,AD,AC的中点,AC=BC,∠ACD=90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 12 | C. | 8 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
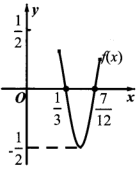 函数f(x)=$\frac{1}{2}$sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )
函数f(x)=$\frac{1}{2}$sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )| A. | $(-\frac{1}{24}+2kπ,\frac{5}{24}+2kπ)$,(k∈Z) | B. | $(-\frac{1}{12}+\frac{k}{2},\frac{5}{12}+\frac{k}{2})$,(k∈Z) | ||
| C. | $(-\frac{1}{12}+2kπ,\frac{1}{3}+2kπ)$,(k∈Z) | D. | $(-\frac{1}{24}+\frac{k}{2},\frac{5}{24}+\frac{k}{2})$,(k∈Z) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com