
分析 (I)根据条件列方程组解出a,b即可得出椭圆的方程;
(II)设直线l方程为x=my+t,联立方程组消元,利用根与系数的关系求出M的坐标,根据距离公式求出|OM|的最值.
解答 解:( I)由题意得$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{2b=2}\\{{a}^{2}-{b}^{2}={c}^{2}}\end{array}\right.$,解得a=2,b=1.
∴椭圆C的标准方程$\frac{x^2}{4}+{y^2}=1$.
( II)设A(x1,y1),B(x2,y2),M(x0,y0),
若直线l的斜率为0,则l方程为y=±1,此时直线l与椭圆只有1个交点,不符合题意;
设直线l:x=my+t.
∵l与圆O相切,∴$\frac{{|{-t}|}}{{\sqrt{1+{m^2}}}}=1$,即t2=m2+1;
联立方程组$\left\{\begin{array}{l}{x^2}+4{y^2}=4\\ x=my+t\end{array}\right.$,消去x,得(m2+4)y2+2mty+t2-4=0,
则△=4m2t2-4(t2-4)(m2+4)=16(m2-t2+4)=48>0,
∴${y_1}+{y_2}=-\frac{2mt}{{{m^2}+4}}$,∴${y_0}=-\frac{mt}{{{m^2}+4}}$,${x_0}=m{y_0}+t=\frac{4t}{{{m^2}+4}}$,即$M(\frac{4t}{{{m^2}+4}},-\frac{mt}{{{m^2}+4}})$,
∴${|{OM}|^2}={(\frac{4t}{{{m^2}+4}})^2}+{(\frac{mt}{{{m^2}+4}})^2}=\frac{{{t^2}({m^2}+16)}}{{{{({m^2}+4)}^2}}}=\frac{{({m^2}+1)({m^2}+16)}}{{{{({m^2}+4)}^2}}}$,
设x=m2+4,则x≥4,${|{OM}|^2}=\frac{(x-3)(x+12)}{x^2}=-\frac{36}{x^2}+\frac{9}{x}+1=-36{(\frac{1}{x}-\frac{1}{8})^2}+\frac{25}{16}≤\frac{25}{16}$,
∴当x=8时等号成立,|OM|取得最大值$\sqrt{\frac{25}{16}}$=$\frac{5}{4}$.
点评 本题考查了椭圆的性质,直线与椭圆的位置关系,注意根与系数的关系应用,属于中档题,


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{9}{5}$] | B. | (-∞,3] | C. | [$\frac{9}{5}$,+∞) | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
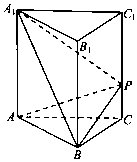
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
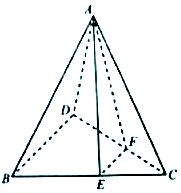 如图,在三棱锥A-BCD中,E,F分别为BC,CD上的点,且BD∥平面AEF.
如图,在三棱锥A-BCD中,E,F分别为BC,CD上的点,且BD∥平面AEF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
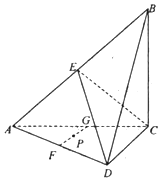 如图,在四面体ABCD中,平面ABC⊥平面ACD,E,F,G分别为AB,AD,AC的中点,AC=BC,∠ACD=90°.
如图,在四面体ABCD中,平面ABC⊥平面ACD,E,F,G分别为AB,AD,AC的中点,AC=BC,∠ACD=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com