
分析 (I)由椭圆右焦点F(1,0),△MCD的面积是△NCD的面积的3倍,求出a,b,由此能求出椭圆Γ的方程.
(II)法一:当∠ACD=∠BCD,则kAC+kBC=0,设直线AC的斜率为k,则直线BC的斜率为-k,则AC的直线方程为$y-\frac{3}{2}=k({x-1})$,代入$\frac{x^2}{4}+\frac{y^2}{3}=1$中整理得(3+4k2)x2-4k(2k-3)x+4k2-12k-3=0,由此能求出直线AB的斜率是定值$\frac{1}{2}$.
法二:设AB方程:y=kx+m,代入$\frac{x^2}{4}+\frac{y^2}{3}=1$中,整理得(4k2+3)x2+8kmx+4m2-12=0,由此利用韦达定理、根的判别式、直线方程、椭圆性质,结合已知条件,能求出直线AB的斜率是定值$\frac{1}{2}$.
解答 解:(I)因为椭圆$Γ:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点F(1,0),
所以c=1,
因为△MCD的面积是△NCD的面积的3倍,
所以MF=3NF,即a+c=3(a-c),所以a=2c=2,所以b2=3,
则椭圆Γ的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$. …(4分)
(II)解法一:当∠ACD=∠BCD,则kAC+kBC=0,
设直线AC的斜率为k,则直线BC的斜率为-k,
不妨设点C在x轴上方,$C({1,\frac{3}{2}})$,设A(x1,y1),B(x2,y2),
则AC的直线方程为$y-\frac{3}{2}=k({x-1})$,代入$\frac{x^2}{4}+\frac{y^2}{3}=1$中整理得(3+4k2)x2-4k(2k-3)x+4k2-12k-3=0,$1+{x_1}=\frac{{4k({2k-3})}}{{({3+4{k^2}})}}$;
同理$1+{x_2}=\frac{{4k({2k+3})}}{{({3+4{k^2}})}}$. …(8分)
所以${x_1}+{x_2}=\frac{{8{k^2}-6}}{{({3+4{k^2}})}}$,${x_1}-{x_2}=\frac{-24k}{{({3+4{k^2}})}}$,…(10分)
则${k_{AB}}=\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}$=$\frac{{k({{x_1}+{x_2}})-2k}}{{{x_1}-{x_2}}}$=$\frac{1}{2}$,
因此直线AB的斜率是定值$\frac{1}{2}$. …(12分)
(II)解法二:依题意知直线AB的斜率存在,所以设AB方程:y=kx+m,
代入$\frac{x^2}{4}+\frac{y^2}{3}=1$中,整理得(4k2+3)x2+8kmx+4m2-12=0,
设A(x1,y1),B(x2,y2),
所以${x_1}+{x_2}=-\frac{8km}{{4{k^2}+3}}$,${x_1}{x_2}=\frac{{4{m^2}-12}}{{4{k^2}+3}}$,…(6分)
△=64k2m2-4(4k2+3)(4m2-12)=16(12k2-3m2+9)>0
当∠ACD=∠BCD,则kAC+kBC=0,不妨设点C在x轴上方,$C({1,\frac{3}{2}})$,
所以$\frac{{{y_1}-\frac{3}{2}}}{{{x_1}-1}}+\frac{{{y_2}-\frac{3}{2}}}{{{x_2}-1}}=0$,整理得$2k{x_1}{x_2}+(m-\frac{3}{2})({x_1}+{x_2})-2m+3=0$,…(8分)
所以$2k•\frac{{4{m^2}-12}}{{4{k^2}+3}}+(m-\frac{3}{2})(-\frac{8km}{{4{k^2}+3}})-2m+3=0$,
整理得12k2+12(m-2)k+9-6m=0,…(9分)
即(6k-3)(2k+2m-3)=0,所以2k+2m-3=0或6k-3=0.…(10分)
当2k+2m-3=0时,直线AB过定点$C({1,\frac{3}{2}})$,不合题意;
当6k-3=0时,$k=\frac{1}{2}$,符合题意,
所以直线AB的斜率是定值$\frac{1}{2}$. …(12分)
点评 本题考查椭圆方程、韦达定理、根的判别式、直线方程等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,考查创新意识、应用意识,是中档题.


科目:高中数学 来源: 题型:解答题
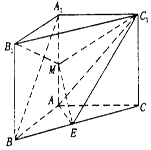 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{|\overrightarrow{a}|}$ | B. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{{\overrightarrow{a}}^{2}}$ | C. | $\frac{{\overrightarrow{b}}^{2}-{\overrightarrow{a}}^{2}}{|\overrightarrow{b}|}$ | D. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{|\overrightarrow{b}|}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\frac{{3\sqrt{6}}}{4}$ | C. | $\sqrt{5}$ | D. | $\frac{{3\sqrt{5}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
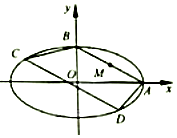 如图,在平面直角坐标系xoy中,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点和上顶点分别为点A,B,M是线段AB的中点,且$\overrightarrow{OM}•\overrightarrow{AB}=-\frac{3}{2}{b^2}$..
如图,在平面直角坐标系xoy中,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点和上顶点分别为点A,B,M是线段AB的中点,且$\overrightarrow{OM}•\overrightarrow{AB}=-\frac{3}{2}{b^2}$..查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2kπ+$\frac{π}{6}$,2kπ+$\frac{5π}{6}$),k∈Z | |
| B. | (2kπ-$\frac{π}{6}$,2kπ)∪(2kπ,2kπ+π)∪(2kπ+π,2kπ+$\frac{7}{6}$π),k∈Z | |
| C. | (2kπ-$\frac{5π}{6}$,2kπ-$\frac{π}{6}$),k∈Z | |
| D. | (2kπ-$\frac{7π}{6}$,2kπ-π)∪(2kπ-π,2kπ)∪(2kπ,2kπ+$\frac{π}{6}$),k∈Z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com