
| A. | $\sqrt{6}$ | B. | $\frac{{3\sqrt{6}}}{4}$ | C. | $\sqrt{5}$ | D. | $\frac{{3\sqrt{5}}}{4}$ |
分析 如图所示,由 切线的性质可得:OQ⊥PF2.又点O为线段F1F2的中点,利用三角形中位线定理可得:OQ∥PF1,PF1⊥PF2.再利用椭圆的定义、勾股定理可得(2b)2+(2a-2b)2=(2c)2,化为:b=$\frac{2a}{3}$.c2=a2-b2=$\frac{5}{9}{a}^{2}$.代入$\frac{{{a^2}+{e^2}}}{b}$,利用基本不等式的性质即可得出.
解答 解:如图所示,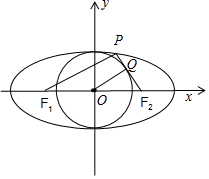 由 切线的性质可得:OQ⊥PF2.
由 切线的性质可得:OQ⊥PF2.
又点O为线段F1F2的中点,Q为线段PF2的中点,
∴OQ∥PF1,∴PF1⊥PF2.
∴|PF1|=2|OQ|=2b,|PF2|=2a-2b.
在Rt△PF1F2中,(2b)2+(2a-2b)2=(2c)2,
化为:b2+(a-b)2=c2=a2-b2,
化为:b=$\frac{2a}{3}$.
∴c2=a2-b2=${a}^{2}-(\frac{2a}{3})^{2}$=$\frac{5}{9}{a}^{2}$.
∴$\frac{{{a^2}+{e^2}}}{b}$=$\frac{{a}^{2}+\frac{{c}^{2}}{{a}^{2}}}{b}$=$\frac{{a}^{4}+\frac{5}{9}{a}^{2}}{{a}^{2}×\frac{2a}{3}}$=$\frac{9{a}^{2}+5}{6a}$≥$\frac{2\sqrt{9{a}^{2}•5}}{6a}$=$\sqrt{5}$,当且仅当a2=$\frac{5}{9}$时取等号.
∴$\frac{{{a^2}+{e^2}}}{b}$(其中e为椭圆C的离心率)的最小值为$\sqrt{5}$.
故选:C.
点评 本题考查了椭圆的定义标准方程与几何性质、三角形中位线定理、勾股定理、基本不等式的性质,考查了推理能力与计算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
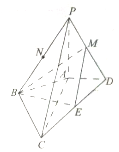 在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N分别为PD,PB,CD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N分别为PD,PB,CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
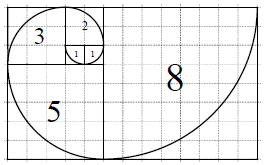 斐波那契数列{an}满足:${a_1}=1,{a_2}=1,{a_n}={a_{n-1}}+{a_{n-2}}({n≥3,n∈{N^*}})$.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前n项所占的格子的面积之和为Sn,每段螺旋线与其所在的正方形所围成的扇形面积为cn,则下列结论错误的是( )
斐波那契数列{an}满足:${a_1}=1,{a_2}=1,{a_n}={a_{n-1}}+{a_{n-2}}({n≥3,n∈{N^*}})$.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前n项所占的格子的面积之和为Sn,每段螺旋线与其所在的正方形所围成的扇形面积为cn,则下列结论错误的是( )| A. | ${S_{n+1}}=a_{n+1}^2+{a_{n+1}}•{a_n}$ | B. | a1+a2+a3+…+an=an+2-1 | ||
| C. | a1+a3+a5+…+a2n-1=a2n-1 | D. | 4(cn-cn-1)=πan-2•an+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±x | B. | $y=±\sqrt{2}x$ | C. | $y=±\sqrt{3}x$ | D. | y=±2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
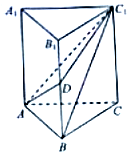 如图,在直三棱柱ABC-A1B1C1中,AB=1,BC=2,BB1=3,∠ABC=90°,点D为侧棱BB1上的动点,当AD+DC1最小时,三棱锥D-ABC1的体积为$\frac{1}{3}$.
如图,在直三棱柱ABC-A1B1C1中,AB=1,BC=2,BB1=3,∠ABC=90°,点D为侧棱BB1上的动点,当AD+DC1最小时,三棱锥D-ABC1的体积为$\frac{1}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com