练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．已知对于任意的x∈（-∞，1）∪（5，+∞），都有x2-2（a-2）x+a＞0，则实数a的取值范围是（1，5]．

    分析 对△进行讨论，利用二次函数的性质列不等式解出．

    解答 解：△=4（a-2）2-4a=4a2-20a+16=4（a-1）（a-4）．
    （1）若△＜0，即1＜a＜4时，x2-2（a-2）x+a＞0在R上恒成立，符合题意；
    （2）若△=0，即a=1或a=4时，方程x2-2（a-2）x+a＞0的解为x≠a-2，
    显然当a=1时，不符合题意，当a=4时，符合题意；
    （3）当△＞0，即a＜1或a＞4时，∵x2-2（a-2）x+a＞0在（-∞，1）∪（5，+∞）恒成立，
    ∴$\left\{\begin{array}{l}{1-2（a-2）+a≥0}\\{25-10（a-2）+a≥0}\\{1＜a-2＜5}\end{array}\right.$，解得3＜a≤5，
    又a＜1或a＞4，∴4＜a≤5．
    综上，a的范围是（1，5]．
    故答案为（1，5]．

    点评 本题考查了二次函数与二次不等式的关系，二次函数的性质，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    14．某销售公司为了解员工的月工资水平，从1000位员工中随机抽取100位员工进行调查，得到如下的频率分布直方图：
    （1）试由此图估计该公司员工的月平均工资；
    （2）该公司工资发放是以员工的营销水平为重要依据来确定的，一般认为，工资低于4500元的员工属于学徒阶段，没有营销经验，若进行营销将会失败；高于4500元的员工是具备营销成熟员工，进行营销将会成功．现将该样本按照“学徒阶段工资”、“成熟员工工资”分为两层，进行分层抽样，从中抽出5人，在这5人中任选2人进行营销活动．活动中，每位员工若营销成功，将为公司赢得3万元，否则公司将损失1万元，试问在此次比赛中公司收入多少万元的可能性最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

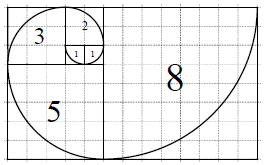    15．斐波那契数列{an}满足：${a_1}=1，{a_2}=1，{a_n}={a_{n-1}}+{a_{n-2}}（{n≥3，n∈{N^*}}）$．若将数列的每一项按照下图方法放进格子里，每一小格子的边长为1，记前n项所占的格子的面积之和为Sn，每段螺旋线与其所在的正方形所围成的扇形面积为cn，则下列结论错误的是（　　）
    A．${S_{n+1}}=a_{n+1}^2+{a_{n+1}}•{a_n}$B．a1+a2+a3+…+an=an+2-1
    C．a1+a3+a5+…+a2n-1=a2n-1D．4（cn-cn-1）=πan-2•an+1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知椭圆$Γ：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的右焦点F（1，0），椭圆Γ的左，右顶点分别为M，N．过点F的直线l与椭圆交于C，D两点，且△MCD的面积是△NCD的面积的3倍．
    （Ⅰ）求椭圆Γ的方程；
    （Ⅱ）若CD与x轴垂直，A，B是椭圆Γ上位于直线CD两侧的动点，且满足∠ACD=∠BCD，试问直线AB的斜率是否为定值，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知一组数据3，6，9，8，4，则该组数据的方差是5.2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．甲盒子中有编号分别为1，2的两个乒乓球，乙盒子中有编号分别为3，4，5，6的四个乒乓球．现分别从两个盒子中随机地各取出1个乒乓球，则取出的乒乓球的编号之和大于6的概率为$\frac{3}{8}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

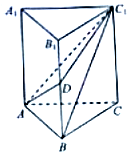    16．如图，在直三棱柱ABC-A1B1C1中，AB=1，BC=2，BB1=3，∠ABC=90°，点D为侧棱BB1上的动点，当AD+DC1最小时，三棱锥D-ABC1的体积为$\frac{1}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．在直角坐标系xOy中，已知点P（2，0），曲线C的参数方程为$\left\{\begin{array}{l}x=4{t^2}\\ y=4t\end{array}\right.$（t为参数）．以坐标原点为极点，x轴正半轴为极轴建立极坐标系．
    （Ⅰ）求曲线C的普通方程和极坐标方程；
    （Ⅱ）过点P且倾斜角为$\frac{π}{4}$的直线l交曲线C于A，B两点，求|AB|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=Asin（ωx+$\frac{π}{3}$）（A＞0，ω＞0）图象的相邻两条对称轴之间的距离为π，且经过点（$\frac{π}{3}$，$\frac{\sqrt{3}}{2}$）
    （1）求函数f（x）的解析式；
    （2）若角α满足f（α）+$\sqrt{3}$f（α-$\frac{π}{2}$）=1，α∈（0，π），求α值．

    查看答案和解析>>

    同步练习册答案