
| A. | (2kπ+$\frac{π}{6}$,2kπ+$\frac{5π}{6}$),k∈Z | |
| B. | (2kπ-$\frac{π}{6}$,2kπ)∪(2kπ,2kπ+π)∪(2kπ+π,2kπ+$\frac{7}{6}$π),k∈Z | |
| C. | (2kπ-$\frac{5π}{6}$,2kπ-$\frac{π}{6}$),k∈Z | |
| D. | (2kπ-$\frac{7π}{6}$,2kπ-π)∪(2kπ-π,2kπ)∪(2kπ,2kπ+$\frac{π}{6}$),k∈Z |
分析 求出f(x)的解析式,确定f(x)=f($\frac{1}{x}$),函数f(x)在(-1,1)上单调递增,(-∞,-1),(1,+∞)上单调递减,不等式转化为sinθ<-cos2θ,即可得出结论.
解答 解:由题意,-f(x)=2g(x)+$\frac{-x-4}{{x}^{2}+1}$,f(x)=2g(x)+$\frac{x-4}{{x}^{2}+1}$,
∴f(x)=$\frac{x}{{x}^{2}+1}$,∴f($\frac{1}{x}$)=$\frac{x}{{x}^{2}+1}$,
又f′(x)=$\frac{1-{x}^{2}}{({x}^{2}+1)^{2}}$,∴函数f(x)在(-1,1)上单调递增,(-∞,-1),(1,+∞)上单调递减
∵f($\frac{1}{sinθ}$)+f(cos2θ)<f(π)-f($\frac{1}{π}$),
∴f($\frac{1}{sinθ}$)+f(cos2θ)<0,
∴f(sinθ)<f(-cos2θ),且sinθ≠0
∴sinθ<-cos2θ,且sinθ≠0
∴2sin2θ-sinθ-1>0,且sinθ≠0
∴sinθ<-$\frac{1}{2}$,且sinθ≠0,
∴θ∈(2kπ-$\frac{5π}{6}$,2kπ-$\frac{π}{6}$),k∈Z,
故选C.
点评 本题考查函数的单调性与奇偶性,考查不等式的解法,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
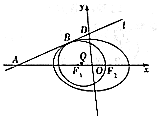 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,过点A(-4,0)的直线l与椭圆C相切于点B,与y轴交于点D(0,2),又椭圆的离心率为$\frac{1}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,过点A(-4,0)的直线l与椭圆C相切于点B,与y轴交于点D(0,2),又椭圆的离心率为$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 3$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 数据 | [12,5,15.5) | [15.5,18.5) | [18.5,21.5) | [21,5,24.5) |
| 频数 | 2 | 1 | 3 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 142 | B. | 124 | C. | 128 | D. | 144 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com