
分析 由题意,f(x)=$\left\{\begin{array}{l}{{x}^{2}-2x,x≥2}\\{-{x}^{2}+2x,x<2}\end{array}\right.$,在(2,+∞)单调递增,x<2,f(x)max=1<f(3)=3.f(2-ln(x+1))>f(3)化为2-ln(x+1)>3,即可解不等式.
解答 解:由题意,f(x)=$\left\{\begin{array}{l}{{x}^{2}-2x,x≥2}\\{-{x}^{2}+2x,x<2}\end{array}\right.$,在(2,+∞)单调递增,
x<2,f(x)max=1<f(3)=3.
∵f(2-ln(x+1))>f(3),∴2-ln(x+1)>3,
∴ln(x+1)<-1,∴0<x+1<$\frac{1}{e}$,
∴-1<x<$\frac{1}{e}$-1,
∴不等式f(2-ln(x+1))>f(3)的解集为{x|-1<x<$\frac{1}{e}$-1},
故答案为{x|-1<x<$\frac{1}{e}$-1}.
点评 此题考查了其他不等式的解法,解决此类问题的关键是正确利用函数的单调性,结合不等式的解法解出x的范围,此知识点是高考考查的重点之一.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
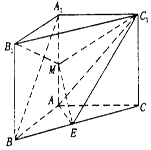 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{|\overrightarrow{a}|}$ | B. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{{\overrightarrow{a}}^{2}}$ | C. | $\frac{{\overrightarrow{b}}^{2}-{\overrightarrow{a}}^{2}}{|\overrightarrow{b}|}$ | D. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{|\overrightarrow{b}|}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
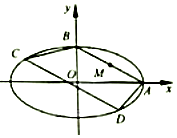 如图,在平面直角坐标系xoy中,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点和上顶点分别为点A,B,M是线段AB的中点,且$\overrightarrow{OM}•\overrightarrow{AB}=-\frac{3}{2}{b^2}$..
如图,在平面直角坐标系xoy中,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点和上顶点分别为点A,B,M是线段AB的中点,且$\overrightarrow{OM}•\overrightarrow{AB}=-\frac{3}{2}{b^2}$..查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com