
分析 (Ⅰ)由椭圆的离心率公式,求得a2=2b2,将P代入椭圆方程,即可求得a和b的值;
(Ⅱ)将直线方程代入椭圆方程,由△>0,求得m的取值范围,利用韦达定理,弦长公式,根二次函数的性质,即可求得△PAB的面积的最大值;
(Ⅲ)设直线PA,PB的斜率分别是k1,k1,根据韦达定理和直线的斜率公式求得k1+k2=0,则∠PMN=∠PNM,则丨PM丨=丨PN丨.
解答 解:(Ⅰ)设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的半焦距为c,
由椭圆C的离心率是e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{{\sqrt{2}}}{2}$,即a2=2b2,[(1分)]
将点$P(\sqrt{2},1)$代入椭圆方程:$\frac{{x}^{2}}{2{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$. 解得$\left\{\begin{array}{l}{{a}^{2}=4}\\{{b}^{2}=2}\end{array}\right.$,[(3分)]
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$;.[(4分)]
(Ⅱ)由$\left\{\begin{array}{l}{y=\frac{\sqrt{2}}{2}x+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,消去y,整理得x2+$\sqrt{2}$mx+m2-2=0.[(5分)]
令△=2m2-4(m2-2)>0,解得-2<m<2.
设A(x1,y1),B(x2,y2),
则x1+x2=-$\sqrt{2}$m,x1x2=m2-2.
∴丨AB丨=$\sqrt{1+{k}^{2}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{3}$•$\sqrt{4-{m}^{2}}$,[(6分)]
点$P(\sqrt{2},1)$.到直线x-$\sqrt{2}$y+$\sqrt{2}$m=0的距离为d=$\frac{丨\sqrt{2}-\sqrt{2}+\sqrt{2}m丨}{\sqrt{1+(\sqrt{2})^{2}}}$=$\frac{\sqrt{2}丨m丨}{\sqrt{3}}$.[(7分)]
∴△PAB的面积S=$\frac{1}{2}$丨AB丨•d=$\frac{\sqrt{2}}{2}$丨m丨•$\sqrt{4-{m}^{2}}$,
=$\frac{\sqrt{2}}{2}$$\sqrt{-({m}^{2}-2)^{2}+4}$≤$\sqrt{2}$,[(8分)]
当且仅当m=±$\sqrt{2}$时,S=$\sqrt{2}$.
则△PAB的面积的最大值$\sqrt{2}$;[(9分)]
(Ⅲ)丨PM丨=丨PN丨.证明如下:[(10分)]
设直线PA,PB的斜率分别是k1,k1,
则k1+k2=$\frac{{y}_{1}-1}{{x}_{1}-\sqrt{2}}$+$\frac{{y}_{1}-1}{{x}_{2}-\sqrt{2}}$=$\frac{({y}_{1}-1)({x}_{2}-\sqrt{2})+({y}_{1}-1)({x}_{1}-\sqrt{2})}{({x}_{1}-\sqrt{2})({x}_{2}-\sqrt{2})}$,[(11分)]
由(Ⅱ)得(y1-1)(x2-$\sqrt{2}$)+(y2-1)(x1-$\sqrt{2}$),
=($\frac{{\sqrt{2}}}{2}$x1+m-1)(x2-$\sqrt{2}$)+($\frac{{\sqrt{2}}}{2}$x1+m-1)(x1-$\sqrt{2}$),
=$\sqrt{2}$x1x2+(m-2)(x1+x2)-2$\sqrt{2}$(m-1),
=$\sqrt{2}$(m2-2)+(m-2)(-$\sqrt{2}$m)-2$\sqrt{2}$(m-1)=0,
∴直线PA,PB的倾斜角互补.[(13分)]
∴∠1=∠2,
∴∠PMN=∠PNM.
∴丨PM丨=丨PN丨.[(14分)]
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,弦长公式,考查椭圆与二次函数取值最值的综合应用,考查计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某销售公司为了解员工的月工资水平,从1000位员工中随机抽取100位员工进行调查,得到如下的频率分布直方图:
某销售公司为了解员工的月工资水平,从1000位员工中随机抽取100位员工进行调查,得到如下的频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
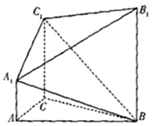 如图,在几何体A1B1C1-ABC中,∠ACB=90°,AC=BC=2,AA1⊥平面ABC,AA1∥BB1∥CC1,BB1:CC1:AA1=3:2:1,且AA1=1.
如图,在几何体A1B1C1-ABC中,∠ACB=90°,AC=BC=2,AA1⊥平面ABC,AA1∥BB1∥CC1,BB1:CC1:AA1=3:2:1,且AA1=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
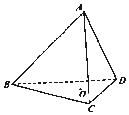 如图,在正四面体ABCD中,O是△BCD的中心,E,F分别是AB,AC上的动点,且$\overrightarrow{BE}$=λ$\overrightarrow{BA}$,$\overrightarrow{CF}$=(1-λ)$\overrightarrow{CA}$
如图,在正四面体ABCD中,O是△BCD的中心,E,F分别是AB,AC上的动点,且$\overrightarrow{BE}$=λ$\overrightarrow{BA}$,$\overrightarrow{CF}$=(1-λ)$\overrightarrow{CA}$查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com