
分析 P在渐近线y=-$\frac{b}{a}x$上,根据$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=0可知OP=c,从而可求出P点坐标,得出PA⊥AB,故PA=AB,从而得出a,b的关系,代入离心率公式计算即可.
解答 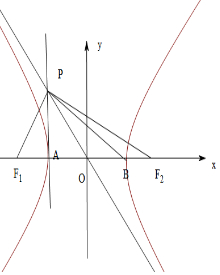 解:由题意可知P在渐近线y=-$\frac{b}{a}x$上,∴y0=-$\frac{b}{a}{x}_{0}$,
解:由题意可知P在渐近线y=-$\frac{b}{a}x$上,∴y0=-$\frac{b}{a}{x}_{0}$,
∵$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=0,∴PF1⊥PF2,
∴OP=$\frac{1}{2}$F1F2=c,即x02+$\frac{{b}^{2}}{{a}^{2}}{{x}_{0}}^{2}$=c2,∴x02=a2,
∴PA⊥x轴,PA=b,
∵∠PBF1=45°,
∴PA=AB,即2a=b,
∴e=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}+4{a}^{2}}}{a}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题考查了双曲线的性质,属于中档题.


科目:高中数学 来源: 题型:选择题
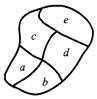 某社区新建了一个休闲小公园,几条小径将公园分成5块区域,如图,社区准备从4种颜色不同的花卉中选择若干种种植在各块区域,要求每个区域随机用一种颜色的花卉,且相邻区域(用公共边的)所选花卉颜色不能相同,则不同种植方法的种数共有( )
某社区新建了一个休闲小公园,几条小径将公园分成5块区域,如图,社区准备从4种颜色不同的花卉中选择若干种种植在各块区域,要求每个区域随机用一种颜色的花卉,且相邻区域(用公共边的)所选花卉颜色不能相同,则不同种植方法的种数共有( )| A. | 96 | B. | 114 | C. | 168 | D. | 240 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 价格x(百元) | 4 | 5 | 6 | 7 | 8 | 9 |
| 销量y(件/天) | 90 | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
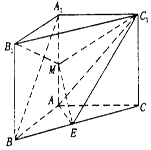 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com