练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．等比数列{an}的前n项和为Sn，Sn=b（-2）n-1-a，则$\frac{a}{b}$=-$\frac{1}{2}$．

    分析 利用递推关系、等比数列的定义与通项公式即可得出．

    解答 解：n=1时，a1=b-a．
    n≥2时，an=Sn-Sn-1=b（-2）n-1-a-[b（-2）n-2-a]，
    上式对于n=1时也成立，可得：b-a=b+$\frac{b}{2}$．
    则$\frac{a}{b}$=-$\frac{1}{2}$．
    故答案为：-$\frac{1}{2}$．

    点评 本题考查了递推关系、等比数列的定义与通项公式，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    15．如果一条信息有n（n＞1，n∈N）种可能的情形（各种情形之间互不相容），且这些情形发生的概率分别为p1，p2，…，pn，则称H=f（p1）+f（p2）+…f（pn）（其中f（x）=-xlogax，x∈（0，1））为该条信息的信息熵．已知$f（\frac{1}{2}）=\frac{1}{2}$．
    （1）若某班共有32名学生，通过随机抽签的方式选一名学生参加某项活动，试求“谁被选中”的信息熵的大小；
    （2）某次比赛共有n位选手（分别记为A1，A2，…，An）参加，若当k=1，2，…，n-1时，选手Ak获得冠军的概率为2-k，求“谁获得冠军”的信息熵H关于n的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．若a＞0，b＞0，4a+b=ab．
    （Ⅰ）求a+b的最小值；
    （Ⅱ）当a+b取得最小值时，a，b的值满足不等式|x-a|+|x-b|≥t2-2t对任意的x∈R恒成立，求t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知函数f（x）=2sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的图象过点B（0，-1），且在（$\frac{π}{18}$，$\frac{π}{3}$）上单调，同时f（x）的图象向左平移π个单位之后与原来的图象重合，当x1，x2∈（-$\frac{17π}{12}$，-$\frac{2π}{3}$），且x1≠x2时，f（x1）=f（x2），则f（x1+x2）=（　　）
    A．-$\sqrt{3}$B．-1C．1D．$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知函数f（x）=lnx，F（x）=x+$\frac{1}{x}$+af′（x）
    （Ⅰ）当a=1时，求M（x）=F（x）-f（x）的极值；
    （Ⅱ）当a=0时，对任意x＞0，$\frac{1}{F（x）}$≤$\frac{1}{2+m[f（x）]^{2}}$恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知A、B为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的左右顶点，F1，F2为其左右焦点，双曲线的渐近线上一点P（x0，y0）（x0＜0，y0＞0），满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=0，且∠PBF1=45°，则双曲线的离心率为$\sqrt{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

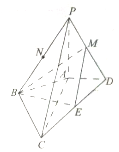    17．在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥BD，PA=AC=2AD=4，AB=BC=2$\sqrt{5}$，M，N分别为PD，PB，CD的中点．
    （1）求证：平面MBE⊥平面PAC；
    （2）求三棱锥B-AME的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．某销售公司为了解员工的月工资水平，从1000位员工中随机抽取100位员工进行调查，得到如下的频率分布直方图：
    （1）试由此图估计该公司员工的月平均工资；
    （2）该公司工资发放是以员工的营销水平为重要依据来确定的，一般认为，工资低于4500元的员工属于学徒阶段，没有营销经验，若进行营销将会失败；高于4500元的员工是具备营销成熟员工，进行营销将会成功．现将该样本按照“学徒阶段工资”、“成熟员工工资”分为两层，进行分层抽样，从中抽出5人，在这5人中任选2人进行营销活动．活动中，每位员工若营销成功，将为公司赢得3万元，否则公司将损失1万元，试问在此次比赛中公司收入多少万元的可能性最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

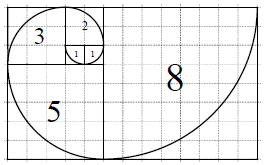    15．斐波那契数列{an}满足：${a_1}=1，{a_2}=1，{a_n}={a_{n-1}}+{a_{n-2}}（{n≥3，n∈{N^*}}）$．若将数列的每一项按照下图方法放进格子里，每一小格子的边长为1，记前n项所占的格子的面积之和为Sn，每段螺旋线与其所在的正方形所围成的扇形面积为cn，则下列结论错误的是（　　）
    A．${S_{n+1}}=a_{n+1}^2+{a_{n+1}}•{a_n}$B．a1+a2+a3+…+an=an+2-1
    C．a1+a3+a5+…+a2n-1=a2n-1D．4（cn-cn-1）=πan-2•an+1

    查看答案和解析>>

    同步练习册答案