
| A. | -$\sqrt{3}$ | B. | -1 | C. | 1 | D. | $\sqrt{3}$ |
分析 由题意求得φ、ω的值,写出函数f(x)的解析式,求图象的对称轴,得x1+x2的值,再求f(x1+x2)的值.
解答 解:由函数f(x)=2sin(ωx+φ)的图象过点B(0,-1),
∴2sinφ=-1,解得sinφ=-$\frac{1}{2}$,
又|φ|<$\frac{π}{2}$,∴φ=-$\frac{π}{6}$,
∴f(x)=2sin(ωx-$\frac{π}{6}$);
又f(x)的图象向左平移π个单位之后为
g(x)=2sin[ω(x+π)-$\frac{π}{6}$]=2sin(ωx+ωπ-$\frac{π}{6}$),
由两函数图象完全重合知ωπ=2kπ,∴ω=2k,k∈Z;
又$\frac{π}{3}$-$\frac{π}{18}$≤$\frac{T}{2}$=$\frac{π}{ω}$,
∴ω≤$\frac{18}{5}$,∴ω=2;
∴f(x)=2sin(2x-$\frac{π}{6}$),其图象的对称轴为x=$\frac{kπ}{2}$+$\frac{π}{3}$,k∈Z;
当x1,x2∈(-$\frac{17π}{12}$,-$\frac{2π}{3}$),其对称轴为x=-3×$\frac{π}{2}$+$\frac{π}{3}$=-$\frac{7π}{6}$,
∴x1+x2=2×(-$\frac{7π}{6}$)=-$\frac{7π}{3}$,
∴f(x1+x2)=f(-$\frac{7π}{3}$)
=2sin[2×(-$\frac{7π}{3}$)-$\frac{π}{6}$]
=2sin(-$\frac{29π}{6}$)
=-2sin$\frac{29π}{6}$
=-2sin$\frac{5π}{6}$=-1.
应选:B.
点评 本题主要考查了三角函数的图象变换和性质的应用问题,也考查了运算求解能力,是综合题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
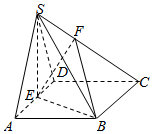 已知四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,SA=SD=$\sqrt{5},SB=\sqrt{7}$,点E是棱AD的中点,点F在棱SC上,且$\frac{SF}{SC}$=λ,SA∥平面BEF.
已知四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,SA=SD=$\sqrt{5},SB=\sqrt{7}$,点E是棱AD的中点,点F在棱SC上,且$\frac{SF}{SC}$=λ,SA∥平面BEF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要 | B. | 必要不充分 | ||
| C. | 充分不必要 | D. | 既不充分也不必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 价格x(百元) | 4 | 5 | 6 | 7 | 8 | 9 |
| 销量y(件/天) | 90 | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
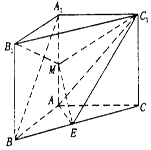 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{|\overrightarrow{a}|}$ | B. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{{\overrightarrow{a}}^{2}}$ | C. | $\frac{{\overrightarrow{b}}^{2}-{\overrightarrow{a}}^{2}}{|\overrightarrow{b}|}$ | D. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{|\overrightarrow{b}|}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com