
分析 (1)由$f(\frac{1}{2})=\frac{1}{2}$,可得$-\frac{1}{2}{log_a}\frac{1}{2}=\frac{1}{2}$,解之得a=2,由32种情形等可能,故${P_k}=\frac{1}{32}(k=1,2,…,32)$,即可求“谁被选中”的信息熵的大小;
(2)$H=\frac{1}{2}+\frac{2}{4}+\frac{3}{8}+…+\frac{n-1}{{{2^{n-1}}}}+\frac{n-1}{{{2^{n-1}}}}$,利用错位相减法,可得结论.
解答 解:(1)由$f(\frac{1}{2})=\frac{1}{2}$,可得$-\frac{1}{2}{log_a}\frac{1}{2}=\frac{1}{2}$,解之得a=2.…(2分)
由32种情形等可能,故${P_k}=\frac{1}{32}(k=1,2,…,32)$,…(4分)
所以$H=32×(-\frac{1}{32}{log_2}\frac{1}{32})=5$,
答:“谁被选中”的信息熵为5. …(6分)
(2)An获得冠军的概率为$1-(\frac{1}{2}+\frac{1}{4}+…+\frac{1}{{{2^{n-1}}}})=1-(1-\frac{1}{{{2^{n-1}}}})=\frac{1}{{{2^{n-1}}}}$,…(8分)
当k=1,2,…,n-1时,$f({p_k})=-{2^{-k}}{log_2}{2^{-k}}=\frac{k}{2^k}$,又$f({p_n})=\frac{n-1}{{{2^{n-1}}}}$,
故$H=\frac{1}{2}+\frac{2}{4}+\frac{3}{8}+…+\frac{n-1}{{{2^{n-1}}}}+\frac{n-1}{{{2^{n-1}}}}$,…(11分)$\frac{1}{2}H=\frac{1}{4}+\frac{2}{8}+…+\frac{n-2}{{{2^{n-1}}}}+\frac{n-1}{2^n}+\frac{n-1}{2^n}$,
以上两式相减,可得$\frac{1}{2}H=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+…+\frac{1}{{{2^{n-1}}}}=1-\frac{1}{{{2^{n-1}}}}$,故$H=2-\frac{4}{2^n}$,
答:“谁获得冠军”的信息熵为$2-\frac{4}{2^n}$. …(14分)
点评 本题考查新定义,考查数列知识的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
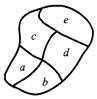 某社区新建了一个休闲小公园,几条小径将公园分成5块区域,如图,社区准备从4种颜色不同的花卉中选择若干种种植在各块区域,要求每个区域随机用一种颜色的花卉,且相邻区域(用公共边的)所选花卉颜色不能相同,则不同种植方法的种数共有( )
某社区新建了一个休闲小公园,几条小径将公园分成5块区域,如图,社区准备从4种颜色不同的花卉中选择若干种种植在各块区域,要求每个区域随机用一种颜色的花卉,且相邻区域(用公共边的)所选花卉颜色不能相同,则不同种植方法的种数共有( )| A. | 96 | B. | 114 | C. | 168 | D. | 240 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
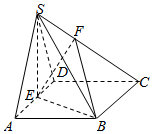 已知四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,SA=SD=$\sqrt{5},SB=\sqrt{7}$,点E是棱AD的中点,点F在棱SC上,且$\frac{SF}{SC}$=λ,SA∥平面BEF.
已知四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,SA=SD=$\sqrt{5},SB=\sqrt{7}$,点E是棱AD的中点,点F在棱SC上,且$\frac{SF}{SC}$=λ,SA∥平面BEF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com