
���� ��1����a1+b2=a2+b3=a3+b1�����õȲ�������ȱ����е�ͨ�ʽ�ɵã�a1+b1q=${a}_{1}+d+{b}_{1}{q}^{2}$=a1+2d+b1�����������ɵó���
��2��am+bp=ap+br=ar+bm����ap-am=bp-br���ɵã�p-m��d=bm��qp-m-qr-m����ͬ���ɵã���r-p��d=bm��qr-m-1������m��p��r�ɵȲ����У��ɵ�p-m=r-p=$\frac{1}{2}$��r-m������qp-m=t�����t=$\frac{1}{2}$����qp-m=$\frac{1}{2}$����-1��q��0����p-m=������Ϊ�������ɹ������1������3���ɵ�|q|=$��\frac{1}{2}��^{\frac{1}{��}}$��$��\frac{1}{2}��^{\frac{1}{3}}$����q$��-��\frac{1}{2}��^{\frac{1}{3}}$�����ɵó���
��3���������������ΪE=��m��m+2��m+3������ʱͨ�ʽΪ��an=$��-\frac{1}{2}��^{m-1}$$��\frac{3}{8}n-\frac{3}{8}m-1��$��m��N*��
��� �⣺��1����a1+b2=a2+b3=a3+b1����a1+b1q=${a}_{1}+d+{b}_{1}{q}^{2}$=a1+2d+b1����Ϊ��2q2-q-1=0��q�١�1��
���q=-$\frac{1}{2}$��
��2��am+bp=ap+br=ar+bm����ap-am=bp-br���ࣨp-m��d=bm��qp-m-qr-m����
ͬ���ɵã���r-p��d=bm��qr-m-1����
��m��p��r�ɵȲ����У���p-m=r-p=$\frac{1}{2}$��r-m������qp-m=t����2t2-t-1=0��
��q�١�1��t�١�1�����t=$\frac{1}{2}$����qp-m=$\frac{1}{2}$����-1��q��0��
��p-m=������Ϊ�������ɹ������1�������3��
��|q|=$��\frac{1}{2}��^{\frac{1}{��}}$��$��\frac{1}{2}��^{\frac{1}{3}}$����q$��-��\frac{1}{2}��^{\frac{1}{3}}$��
����=3ʱ��qȡ�����ֵΪ-$��\frac{1}{2}��^{\frac{1}{3}}$��
��3���������������ΪE=��m��m+2��m+3������ʱͨ�ʽΪ��an=$��-\frac{1}{2}��^{m-1}$$��\frac{3}{8}n-\frac{3}{8}m-1��$��m��N*��
����E=��1��3��4����an=$\frac{3}{8}n-\frac{11}{8}$��
���� ���⿼���˵Ȳ�������ȱ����е�ͨ�ʽ�������ʡ�����ʽ�����ʣ���������������������������������⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
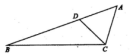 ��ͼ���ڡ�ABC�У�DΪ�߶�AB�ϵĵ㣬��AB=3AD��AC=AD��CB=3CD����$\frac{sin2B}{sinA}$=$\frac{7}{9}$��
��ͼ���ڡ�ABC�У�DΪ�߶�AB�ϵĵ㣬��AB=3AD��AC=AD��CB=3CD����$\frac{sin2B}{sinA}$=$\frac{7}{9}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2+i | B�� | 2-i | C�� | -1+2i | D�� | 1-2i |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com