
分析 利用数列递推关系可得an,再利用指数运算性质、等差数列的求和公式即可得出.
解答 解:∵数列{an}满足lna1+$\frac{{ln{a_2}}}{2}+\frac{{ln{a_3}}}{3}+…+\frac{{ln{a_n}}}{n}$=2n,
∴n≥2时,lna1+$\frac{ln{a}_{2}}{2}$+…+$\frac{ln{a}_{n-1}}{n-1}$=2(n-1),
相减可得:$\frac{ln{a}_{n}}{n}$=2,可得an=e2n.
n=1时,lna1=2,可得a1=e2.
∴数列{an}的前项的乘积=e2+4+…+2n=${e}^{\frac{n(2+2n)}{2}}$=en(n+1).
故答案为:en(n+1).
点评 本题考查了数列递推关系、指数运算性质、等差数列的求和公式,考查了推理能力与计算能力,属于中档题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
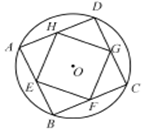 如图,ABCD是以O为圆心、半径为2的圆的内接正方形,EFGH是正方形ABCD的内接正方形,且E、F、G、H分别为AB、BC、CD、DA的中点.将一枚针随机掷到圆O内,用M表示事件“针落在正方形ABCD内”,N表示事件“针落在正方形EFGH内”,则P(N|M)=( )
如图,ABCD是以O为圆心、半径为2的圆的内接正方形,EFGH是正方形ABCD的内接正方形,且E、F、G、H分别为AB、BC、CD、DA的中点.将一枚针随机掷到圆O内,用M表示事件“针落在正方形ABCD内”,N表示事件“针落在正方形EFGH内”,则P(N|M)=( )| A. | $\frac{1}{π}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2+i | B. | 2-i | C. | -1+2i | D. | 1-2i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,四边形ABCD为直角梯形,∠ABC=90°,CB∥DA,AB=20$\sqrt{2}$,DA=10,CB=20,若AB边上有一点P,使得∠CPD最大,则AP=10$\sqrt{2}$.
如图,四边形ABCD为直角梯形,∠ABC=90°,CB∥DA,AB=20$\sqrt{2}$,DA=10,CB=20,若AB边上有一点P,使得∠CPD最大,则AP=10$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com