
分析 (1)求出向量的坐标,再计算数量积;
(2)化简$\overrightarrow{m}•\overrightarrow{n}$,得出cos(2x-$\frac{π}{6}$)=$\frac{\sqrt{3}}{3}$,再利用和角公式计算cos2x.
解答 解:(1)当x=$\frac{π}{3}$时,$\overrightarrow{m}$=($\frac{\sqrt{3}}{2}$,-1),$\overrightarrow{n}$=($\frac{\sqrt{3}}{2}$,$\frac{1}{4}$),
∴$\overrightarrow{m}•\overrightarrow{n}$=$\frac{3}{4}$-$\frac{1}{4}$=$\frac{1}{2}$.
(2)$\overrightarrow{m}•\overrightarrow{n}$=$\sqrt{3}$sinxcosx-cos2x=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$cos2x-$\frac{1}{2}$=sin(2x-$\frac{π}{6}$)-$\frac{1}{2}$,
若$\overrightarrow{m}•\overrightarrow{n}$=$\frac{\sqrt{3}}{3}$-$\frac{1}{2}$,则sin(2x-$\frac{π}{6}$)=$\frac{\sqrt{3}}{3}$,
∵$x∈[{0,\frac{π}{4}}]$,∴2x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{π}{3}$],∴cos(2x-$\frac{π}{6}$)=$\frac{\sqrt{6}}{3}$.
∴cos2x=cos(2x-$\frac{π}{6}$+$\frac{π}{6}$)=cos(2x-$\frac{π}{6}$)cos$\frac{π}{6}$-sin(2x-$\frac{π}{6}$)sin$\frac{π}{6}$=$\frac{\sqrt{6}}{3}×\frac{\sqrt{3}}{2}$-$\frac{\sqrt{3}}{3}×\frac{1}{2}$=$\frac{3\sqrt{2}-\sqrt{3}}{6}$.
点评 本题考查了平面向量的数量积运算,三角函数恒等变换,属于中档题.


科目:高中数学 来源: 题型:解答题
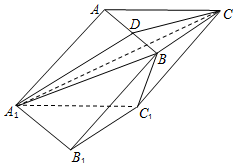 如图,在底边为等边三角形的斜三棱柱ABC-A1B1C1中,AA1=$\sqrt{3}$AB,四边形B1C1CB为矩形,过A1C做与直线BC1平行的平面A1CD交AB于点D.
如图,在底边为等边三角形的斜三棱柱ABC-A1B1C1中,AA1=$\sqrt{3}$AB,四边形B1C1CB为矩形,过A1C做与直线BC1平行的平面A1CD交AB于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
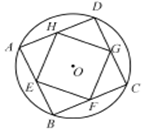 如图,ABCD是以O为圆心、半径为2的圆的内接正方形,EFGH是正方形ABCD的内接正方形,且E、F、G、H分别为AB、BC、CD、DA的中点.将一枚针随机掷到圆O内,用M表示事件“针落在正方形ABCD内”,N表示事件“针落在正方形EFGH内”,则P(N|M)=( )
如图,ABCD是以O为圆心、半径为2的圆的内接正方形,EFGH是正方形ABCD的内接正方形,且E、F、G、H分别为AB、BC、CD、DA的中点.将一枚针随机掷到圆O内,用M表示事件“针落在正方形ABCD内”,N表示事件“针落在正方形EFGH内”,则P(N|M)=( )| A. | $\frac{1}{π}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com